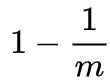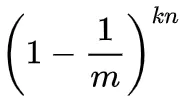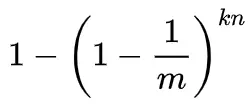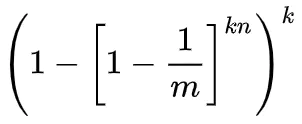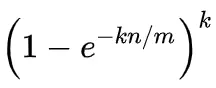Redis的缓存雪崩/缓存穿透/缓存预热+布隆过滤器介绍

Posted on | In , | | 浏览 次
Words count in article: 2.3k | Reading time ≈ 7

Redis作为当下最主流的数据缓存中间件，在实际的运作过程中，有如下几个场景需要特别注意：

1. 缓存雪崩

  • 有时：
    • 缓存集中过期失效。(例如：我们短时间设置大量数据的缓存时采用了相同的过期时间，就会在同一时刻出现大面积的缓存过期)
  • 由于
    • 大量的原本应该访问缓存的请求都因为缓存失效而降级到查询数据库了
  • 导致
    • 短时间内对数据库CPU和内存造成巨大压力，严重的会造成数据库宕机。从而形成一系列连锁反应，造成整个系统崩溃。
  • 解决办法
    • 加锁：大多数系统设计者考虑用加锁（ 最多的解决方案）或者请求队列的方式来保证不会有大量的线程对数据库一次性进行读写，从而避免失效时大量的并发请求落到底层存储系统上。
    • 分散过期时间：还有一个简单方案就是将缓存失效时间分散开，比如加一个随机因子，使过期时间离散。

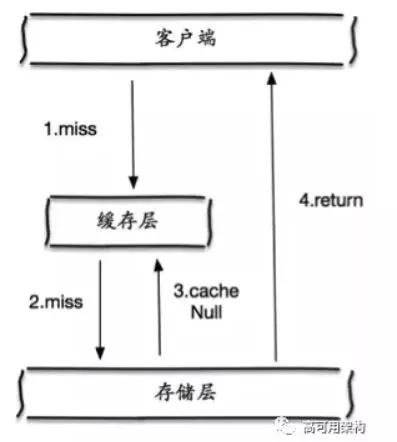
2. 缓存穿透

缓存穿透又叫缓存击穿

  • 有时：
    • 请求查询一个数据库不存在的数据
  • 由于
    • 我们查询数据库结果为空的时候，不会把这个空结果放入缓存
  • 导致
    • 每次查询一个不存在的数据，都不会命中缓存（因为这样的缓存不存在）。促使请求都会降级到数据库上，就像缓存被击穿了一样。
    • 假如有恶意攻击，就可以利用这个漏洞，对数据库造成压力，甚至压垮数据库。即便是采用UUID，也是很容易找到一个不存在的KEY，进行攻击。
  • 解决办法
    • 缓存空值：如果从数据库查询的对象为空，也放入缓存，只是设定的缓存过期时间较短，比如设置为60秒。
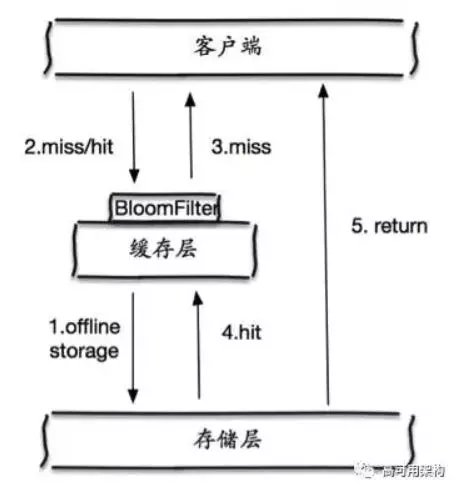
    • 布隆过滤器（Bloom Filter）：推荐！将所有可能存在的key都插入到Bloom Filter中，这样肯定不存在的key就可以被Bloom Filter过滤。

2.1 布隆过滤器

布隆过滤器（Bloom Filter）由Burton Howard Bloom在1970年提出，是一种空间效率高的概率型数据结构。它专门用来快速判断一个元素是否在一个集合中。听起来是很稀松平常的需求，为什么要使用BF这种数据结构呢？

2.1.1 背景

回想一下，我们平常在检测集合中是否存在某元素时，都会采用比较的方法。考虑以下情况：

  • 如果集合用线性表存储，查找的时间复杂度为O(n)。
  • 如果用平衡BST（如AVL树、红黑树）存储，时间复杂度为O(logn)。
  • 如果用哈希表存储，并用链地址法与平衡BST解决哈希冲突（参考JDK8的HashMap实现方法），时间复杂度也要有O[log(n/m)]，m为哈希分桶数。

总而言之，当集合中元素的数量极多时，不仅查找会变得很慢，而且占用的空间也会大到无法想象。Bloom Filter就是解决这个矛盾的利器。

2.1.2 原理

  • Bloom Filter是由一个长度为m的bit数组（bit array）与k个哈希函数（hash function）组成的数据结构。bit数组均初始化为0，所有哈希函数都可以分别把输入数据尽量均匀地散列。

    • 如下图：假设m=10，k=2，即有f1和f2两个哈希函数。

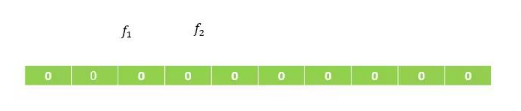
  • 当要插入一个元素时，将其数据分别输入k个哈希函数，产生k个哈希值。以哈希值作为位数组中的下标，将所有k个对应的比特置为1。

    • 如下图，假设输入的数据是N1，经过计算f1(N1)得到的数值得为2，f2(N1)得到的数值为5，则将数组下标为2和下表为5的位置置为1

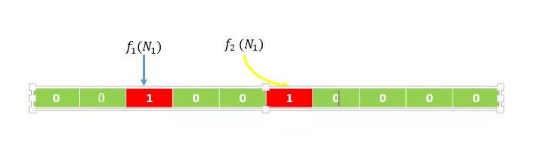
  • 当要查询（即判断是否存在）一个元素时，同样将其数据输入哈希函数，然后检查对应的k个比特。如果有任意一个比特为0，表明该元素一定不在集合中。如果所有比特均为1，表明该集合有（较大的）可能性在集合中。

    • 假设这时候查询N存不存在，将其带入f1和f2，得到结果r1和r2，分别检查r1和r2下标对应的bit数组元素值，假设为b1和b2
      • b1和b2有任意一个比特为0，表明该元素一定不在集合中。
      • b1和b2均为1，表明该集合有（较大的）可能性在集合中。

为什么不是一定在集合中呢？因为一个比特被置为1有可能会受到其他元素的影响，这就是所谓“假阳性”（false positive）。相对地，“假阴性”（false negative）在BF中是绝不会出现的。

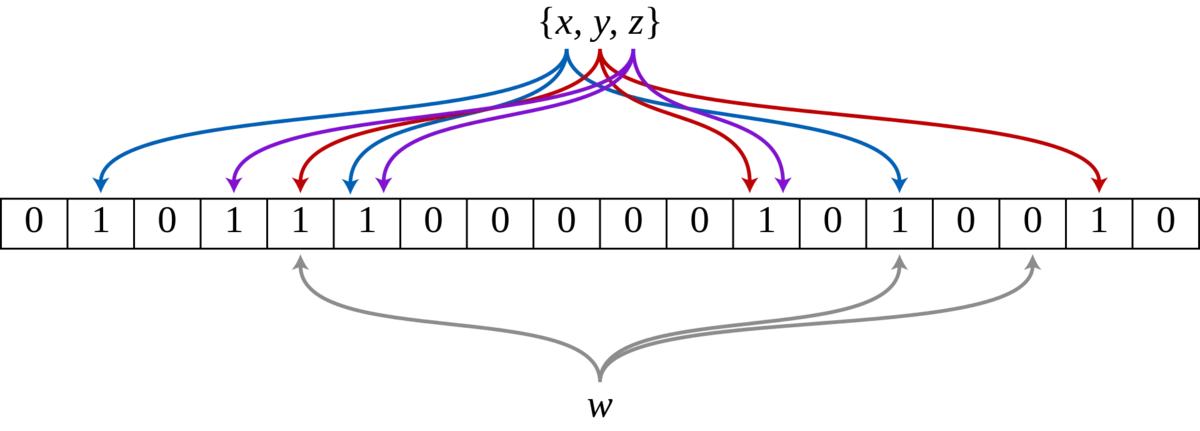
下图示出一个m=18, k=3的BF示例。集合中的x、y、z三个元素通过3个不同的哈希函数散列到位数组中。当查询元素w时，因为有一个比特为0，因此w不在该集合中。

2.1.3 优缺点

BF的优点是显而易见的：

  1. 不需要存储数据本身，只用比特表示，因此空间占用相对于传统方式有巨大的优势，并且能够保密数据；
  2. 时间效率也较高，插入和查询的时间复杂度均为O(k)；
  3. 哈希函数之间相互独立，可以在硬件指令层面并行计算。

但是，它的缺点也同样明显：

  1. 存在假阳性的概率，不适用于任何要求100%准确率的情境；（缓存击穿就不需要100%过滤不存在的key，所以适合）
  2. 只能插入和查询元素，不能删除元素，这与产生假阳性的原因是相同的。我们可以简单地想到通过计数（即将一个比特扩展为计数值）来记录元素数，但仍然无法保证删除的元素一定在集合中。

所以，Bloom Filter在对查准度要求没有那么苛刻，而对时间、空间效率要求较高的场合非常合适，另外，由于它不存在假阴性问题，所以用作“不存在”逻辑的处理时有奇效。目前来看，他有如下三个使用场景:

  • 网页爬虫对URL的去重，避免爬取相同的URL地址
  • 反垃圾邮件，从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱（同理，垃圾短信）
  • 缓存穿透，将所有可能存在的数据缓存放到布隆过滤器中，当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。

2.1.4 假阳性率的计算

假阳性是Bloom Filter最大的痛点，因此有必要权衡，比如计算一下假阳性的概率。为了简单一点，就假设我们的哈希函数选择位数组中的比特时，都是等概率的。当然在设计哈希函数时，也应该尽量满足均匀分布。

  • 在位数组长度m的BF中插入一个元素，它的其中一个哈希函数会将某个特定的比特置为1。因此，在插入元素后，该比特仍然为0的概率是：

  • 现有k个哈希函数，并插入n个元素，自然就可以得到该比特仍然为0的概率是：

  • 反过来讲，它已经被置为1的概率就是：

  • 也就是说，如果在插入n个元素后，我们用一个不在集合中的元素来检测，那么被误报为存在于集合中的概率（也就是所有哈希函数对应的比特都为1的概率）为：

  • 当n比较大时，根据重要极限公式，可以近似得出假阳性率：

所以，在哈希函数的个数k一定的情况下：

  • 位数组长度m越大，假阳性率越低；
  • 已插入元素的个数n越大，假阳性率越高。

有一些框架内已经内建了BF的实现，免去了自己实现的烦恼。比如Guava 27.0.1版本的源码，BF的具体逻辑位于com.google.common.hash.BloomFilter类中

3. 缓存预热

  • 定义
    • 缓存预热是一个比较常见的概念，即系统上线后，将相关的缓存数据直接加载到缓存系统。这样用户就可以直接查询事先被预热的缓存数据，避免在用户请求的时候，先查询数据库，然后再将数据缓存。
  • 解决思路
    1. 直接写个缓存刷新开关，上线时手工操作下；
    2. 数据量不大，可以在项目启动的时候自动进行加载；
    3. 定时刷新缓存；
0%