B树/B+树分析

Posted on | In , | | 浏览 次
Words count in article: 5.8k | Reading time ≈ 20

前言

目前我们常见的动态查找树主要有：二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced Binary Search Tree），红黑树(Red-Black Tree )，这三者是典型的二叉树结构，利用二分法，可以使其查询的时间复杂度为O(log2N)，即与树的深度相关。

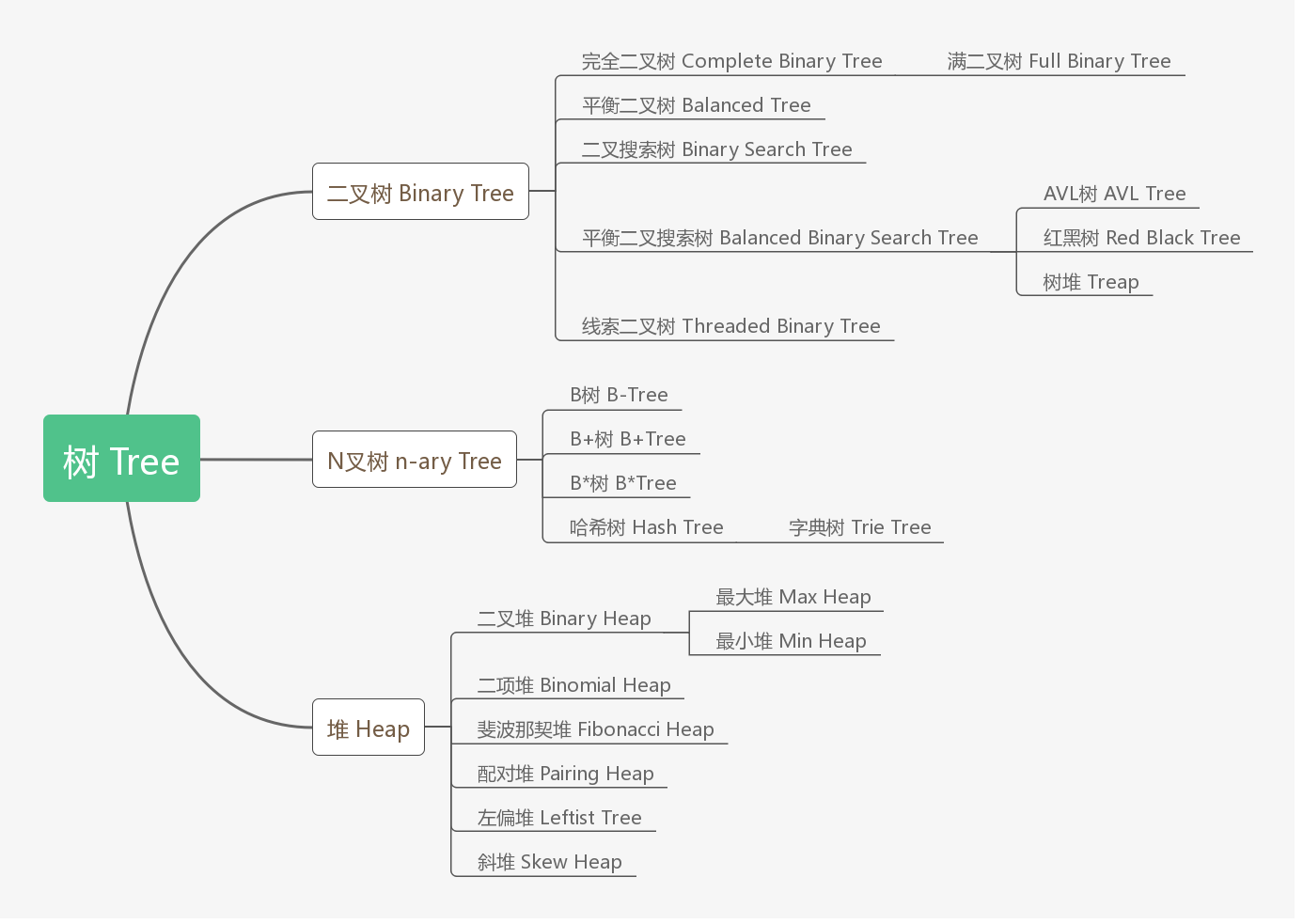
但二叉树一个节点中包含有一个元素，和指向两个子节点的指针，在现实生活中，未免有些太“奢侈”了。为了降低树的深度，提高查找效率，我们完全可以采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）来得到一棵更加“矮胖”的树，以适应我们日益增长的数据量和查询性能要求，在这种背景下，B树和他的亲戚们应运而生。

1. B树

B-tree（B-tree树即B树，B即Balanced，平衡的意思）这棵神奇的树是在Rudolf Bayer, Edward M. McCreight(1970)写的一篇论文《Organization and Maintenance of Large Ordered Indices》中首次提出的（wikipedia中：http://en.wikipedia.org/wiki/B-tree，阐述了B-tree名字来源以及相关的开源地址）。

B树属于多叉树，又名平衡多路查找树（查找路径不只两个），数据库索引技术里大量使用者B树和B+树的数据结构。

强调一下，有的文章里出现的B-树，就是B树。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是一种一种树。而事实上是，B-tree就是指的B树。

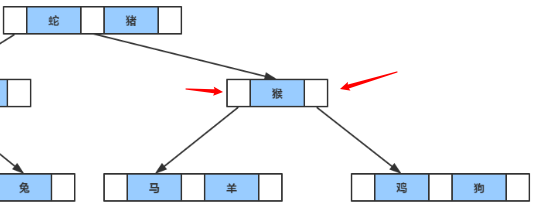
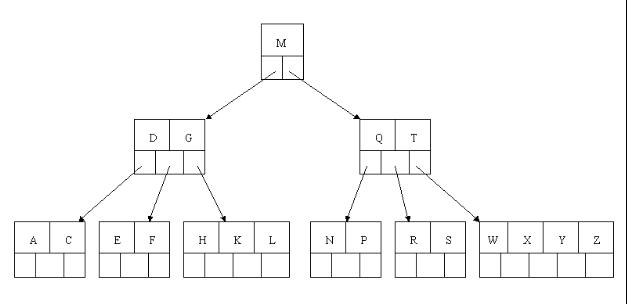
什么是B树？抛出一大堆概念前，我们先看看他长什么样：

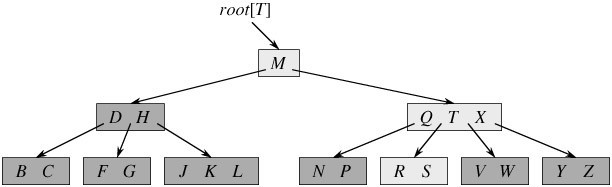
这里面，每个字母，都表示一个键值对[key,value]，在关系型数据库的使用场景中，key一般是索引值（如果是主键索引的话，那就是ID字段，如果是普通索引，那就是索引对应的字段值，如果是联合索引，可以简单理解为对应多个字段的拼接），value一般是指向行数据的指针（聚簇索引是这样）或者主键id（非聚簇索引）；

结合该图，我们可以归纳出B树的规则：

  1. 节点容量：每个节点，都可以容纳多个键值对。
  2. 排序方式：所有节点键值对是按key递增次序排列，并遵循左小右大原则；
  3. 层级结构：所有叶子节点均在同一层
  4. 子树指针：节点中每个键值对的两侧，都可以放置指针（不一定都有值，可以是null），如果有值，则左边指向左子树（key都比当前key小），右边指向右子树（key都比当前key大）

B树种，每个节点最多可以容纳多少个键值对呢？这当然不可能是无限的，在数据结构的定义中，我们引入如下概念来描述：

  1. 度（degree），在树中，每个节点的子树个数就称为该节点的度。（注意是子树数量，而不是键值对的数量）
  2. 阶（order），在树中，一个节点可以拥有的最大子树数量称为阶。（注意是子树数量，而不是键值对的数量）

然而上述的规则，只能得到一个B树，却不一定得到一个平衡的B树，极端一点，下图这样的树，它也可以是个B树，但这显然不是我们想要的。

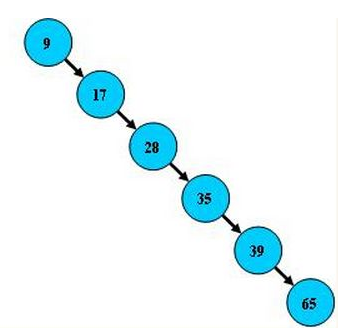
对于一个M阶的平衡的B树，除了上述的规则之外，我们还要加上如下的约束：

  1. 根节点至少有两颗子树
  2. 除根节点和叶子结点外，其他节点至少应该有m/2个子树。
  3. 每个节点的键值对数量k，应该m-1≥k≥ceil(m/2)-1。

ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2

如下图，就是一个5阶的平衡B树，4≥k≥2。

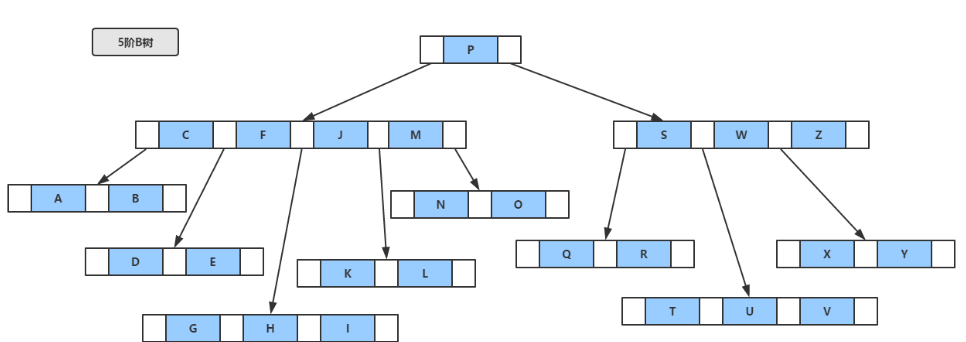
注意，每个节点中的键值对，value都是指向实际data的指针，像下图：

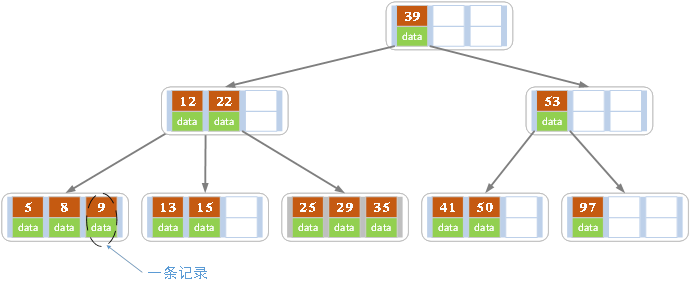
1.1 B树的查询

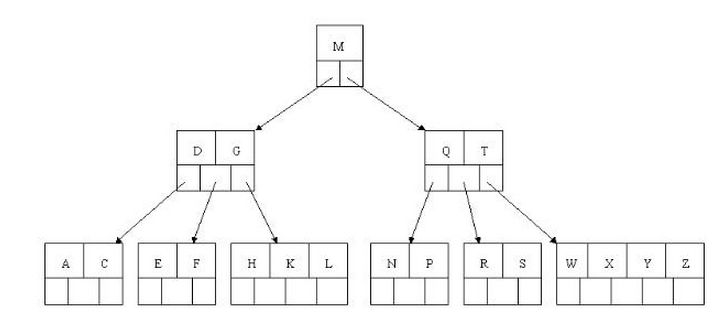
如上图我要从上图中找到E字母，查找流程如下

  1. 获取根节点的关键字进行比较，当前根节点关键字为M，E<M（26个字母顺序），所以往找到指向左边的子节点（二分法规则，左小右大，左边放小于当前节点值的子节点、右边放大于当前节点值的子节点）；

  2. 拿到关键字D和G，D<E<G 所以直接找到D和G中间的节点；

  3. 拿到E和F，因为E=E 所以直接返回关键字和指针信息（如果树结构里面没有包含所要查找的节点则返回null）；

1.2 B树的插入

一棵平衡的B树之所以能维持其平衡性，B树的插入和删除算法功不可没，我们先来看下B树如何应对记录的插入。

对于一个m阶的平衡的B树，从上文我们知道，需要保持其每个节点的键值对数量k为：m-1≥k≥ceil(m/2)-1，新的记录一般是插入在叶子节点上，为了保持这个数量和树的平衡性，我们规定：

  1. 还是按照key递增次序排列，遵循左小右大的原则，在叶子节点上找到新元素的定位。
  2. 若插入时，插入的节点元素个数小于m-1，则该元素直接插入。
  3. 否则，将该节点的元素分裂。

我们下面以5阶B树为例子，在5阶B树中，结点最多有4个键值对，最少有2个键值对。（下面我们把键值对称为元素）

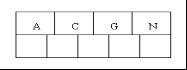
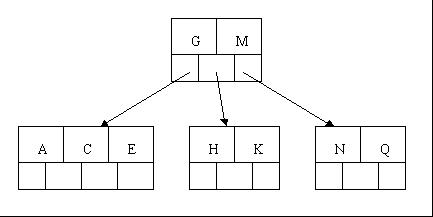
  1. 插入树的第一批元素，A，C，G，N，因为数量不超过4，所以刚好能放在一个节点里面：
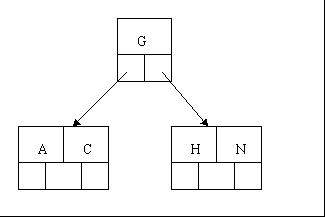
  2. 当试着插入H时，节点发现空间不够（4阶B树，一个节点最多放4个元素），以致将其分裂成2个节点，移动中间元素G上移到新的根节点中，比G元素小的A和C留在当前节点中，而比G元素大的H和N放置新的其右邻居节点中。如下图：
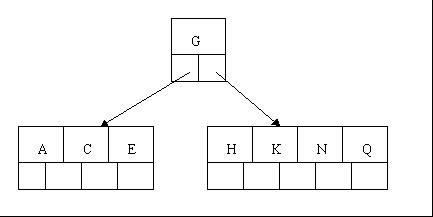
  3. 接下来插入E，K，Q，因为都不触及上界，所以不需要任何分裂操作
  4. 插入M（在K和N之间）就会导致一次分裂，注意M恰好是中间关键字元素，以致向上移到父节点中
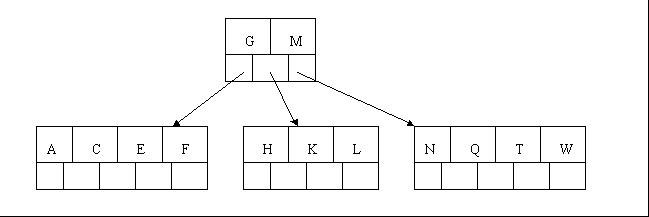
  5. 插入F，W，L，T不需要任何分裂操作
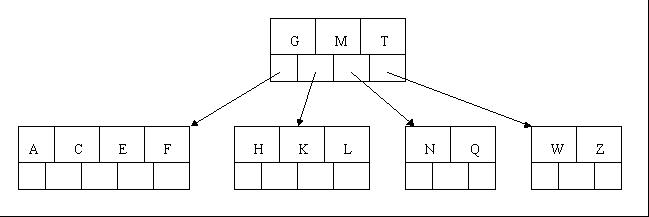
  6. 插入Z时，最右的叶子节点空间满了，需要进行分裂操作，中间元素T上移到父节点中。
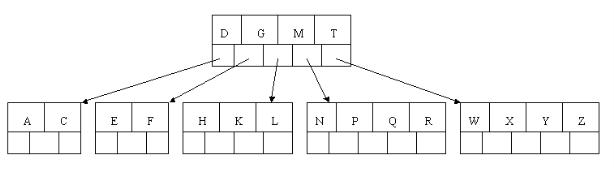
  7. 插入D时，导致最左边的叶子节点被分裂，D恰好也是中间元素，上移到父节点中，然后字母P，R，X，Y陆续插入不需要任何分裂操作
  8. 最后，当插入S时，含有[N,P,Q,R]的节点需要分裂，把中间元素Q上移到父节点中，但是情况来了，父节点中空间已经满了，无法加入Q了，所以也要进行分裂，将父节点中的中间元素M上移到新形成的根结点中。

1.3 B树的删除

B树的删除比插入要更复杂一些，但总体而言，为了保持树的平衡，还是有以下的原则：

分为如下几种情况：

  1. 要删除的记录d在叶子节点上

    • 1.1 如果该节点删除了该元素d后元素数量k仍然大于等于ceil(m/2)-1

      那么这种情况最简单，直接删除元素d和其对应的指针即可。这种情况，我们称为元素直删

    • 1.2 如果该节点删除了元素d后k小于ceil(m/2)-1，那么这时也分两种情况

      • 1.2.1 与该节点相邻的兄弟节点，有任一节点，其k大于等于ceil(m/2)。（这表示即便k-1，也仍然大于等于ceil(m/2)-1）

        那么这种情况，我们应该向兄弟节点，借一个元素过来，但不是简单的借，因为要保证B树元素从左到右递增的顺序，故而借法是有门道的，我们暂称为元素租借。

      • 1.2.2 与该节点相邻的兄弟节点，都没有多余的元素可以借出去，即其k都等于ceil(m/2)-1

        那么这种情况，删除元素d后，我们应该和兄弟节点合并，这样k1=ceil(m/2)-1-1和k2=ceil(m/2)-1,k1+k2还是小于m，符合B树的平衡约束（这也是为什么k的下限是ceil(m/2)-1的原因），这种情况，我们称为元素合并

  2. 要删除的记录d在非叶子节点上

    • 那么这种情况，我们应该在d指针指向的子树中找到一个元素f来替代d的位置，同时在子树中删除f（如果f的删除引起了m-1≥k≥ceil(m/2)-1的不满足，那么操作方法按照情况1：要删除的记录d在叶子节点上来处理），这种情况，我们称为元素顶替

总结之后，我们发现，删除记录的核心操作，就在元素直删，元素租借，元素合并和元素顶替这四个操作步骤之间，直删元素比较简单，我们不多说，剩下的，三种操作步骤，我们来理一下：

我们有一个5阶的b树，原始状态长这样：

  1. 元素顶替
    • 我们先反着来，先删除位于非叶子节点上的记录27
    • 这时候，需要从27的左右指针指向的两棵子树中找元素来置换27，左子树是23,24,26，右子树是28,29
    • 为了保证b树从左到右增序的顺序，所以有资格被置换的元素只有26和28。
    • b树删除的大部分实现，都是采用后继顶替优先原则，即27被删除，则拿27的后继28来顶替。
    • 将28元素替到27原来的位置，同时将右子节点中的28删去，如下图：
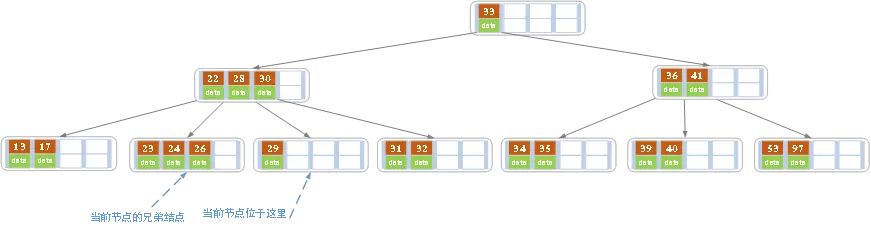
    • 28,29节点删去28之后，显然k小于了ceil(m/2)-1=2，这时候，29有两个兄弟节点：23,24,26和31,32
    • 如果29向23,24,26求援，就会引发元素租借的情况，反之，向31,32求援，就会引发元素合并的情况

其实向哪边求援都可以，实现不同，最终最多导致B树的形态会稍不一样，但肯定的是，他们都是平衡的树。

  1. 元素租借

    • 重申一下， 元素顶替操作结束后，B树长这样
    • 假如29向23,24,26求援，那么23,24,26明显有“余粮”，就会触发租借元素的情况。
    • 23,24,26不能直接将任意一个元素放到29中来，23,24,26任意元素都比28元素小，如果放置在28元素的右子节点上，就违背了左小右大的原则。
    • 那怎么借呢？既然两个当事人23,24,26和29分别是28元素的左右子节点，那就让28元素进入29，26元素替代28元素的位置，这样就皆大欢喜了。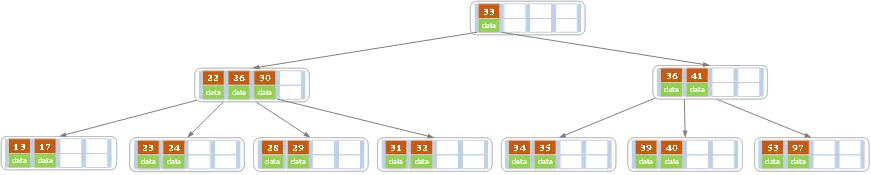

  2. 元素合并

    • 重申一下， 元素顶替操作结束后，B树长这样
    • 假如29向31,32求援，那么31,32明显没有“余粮”，那么就会引发元素合并的情况。
    • 29和31,32不能直接合并，因为30元素还在父节点上，按照左小右大的原则，30元素一定要在29元素和31元素之间
    • 那怎么合并呢？既然两个当事人 29和31,32分别是30元素的左右子节点，那就让30元素与29和31,32一起加入合并，这样就皆大欢喜了。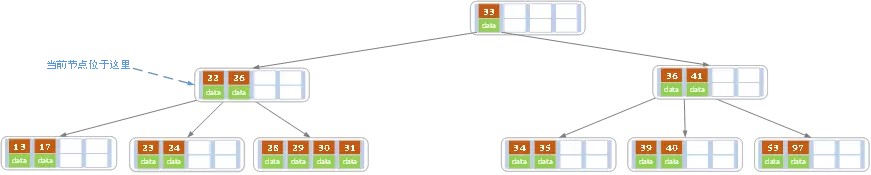

这就结束了么？不是的，大家注意到没有，合并元素操作，其实相当于在父节点中删去了一个元素，如果这一次的删除，导致了父节点的元素数量小于ceil(m/2)-1怎么办？

我们来看这种情况，现在我们的原图长这样：

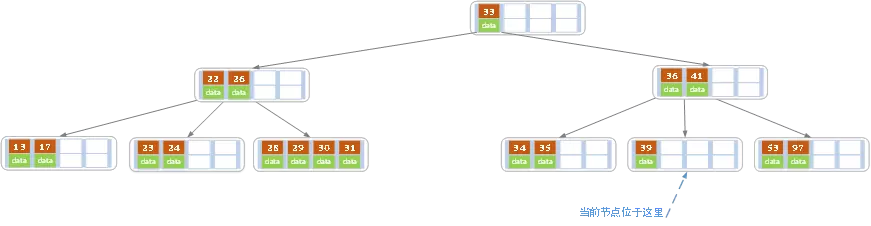
  1. 接着删除key为40的记录，删除后结果如下图所示。

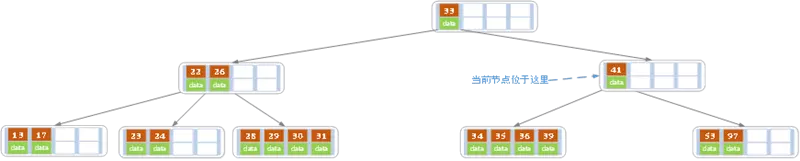
  2. 删完后就剩39一个元素了，没话说，找个兄弟节点合并呗，合并结果如下，可以看到，对于原来的36,41节点来说，相当于36元素被删除了，导致41节点不符合约束。

  3. 这时候，其实有两种策略

    • 一种是采用元素顶替操作：删了我的36，那就拿39顶替呗。
    • 还有一种是向兄弟节点22,26求援，这时要根据兄弟节点的“余粮”情况，酌情触发元素合并或者元素租借。
    • 那到底是采用第一种方案好还是第二种方案好呢？
    • 答案是第二种，因为第二种情况，可能触发元素合并，只要触发元素合并，就有可能降低树的高度，使得B树不仅平衡，而且更加“矮胖”，使查找效率更高。

所以总结一句话，因为元素合并导致的父节点元素数量不符合约束，执行策略时，优先向可能触发元素合并的方向靠拢，有利于使树的高度降低。

1.4 B树的优点

如果经常访问的数据离根节点很近，而B树的非叶子节点本身存有关键字其数据的地址，所以这种数据检索的时候会要比B+树快。

2. B+树

B-Tree有许多变种，其中最常见的是B+Tree，例如MySQL就普遍使用B+Tree实现其索引结构。

B+树是B树的一个升级版，相对于B树来说B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定；我们先看看两者的区别：

  1. B+树的非叶子节点不保存关键字记录的指针，只进行数据索引，这样使得B+树每个非叶子节点所能保存的关键字大大增加；
  2. B+树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样；
  3. B+树叶子节点的关键字从小到大有序排列，左边结尾数据都会保存右边节点开始数据的指针。

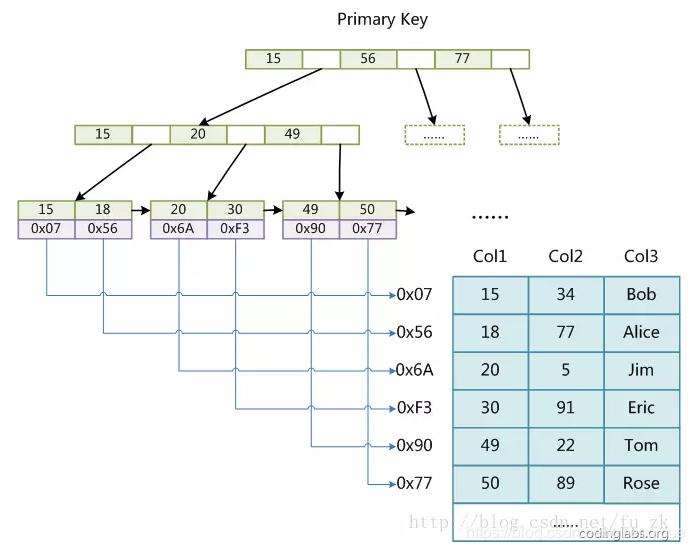
2.1 B+树的插入

B+树的插入操作和B树的插入操作大同小异，即都满足：

  1. 还是按照key递增次序排列，遵循左小右大的原则，在叶子节点上找到新元素的定位。
  2. 若插入时，插入的节点元素个数小于m-1，则该元素直接插入。
  3. 否则，将该节点的元素分裂。

但B+树的叶子节点，会包含所有的元素（不像B树，有些元素在叶子节点上，有些元素在非叶子节点上），所以插入操作有一些许的差异。

我们下面还是以5阶B+树为例子，在5阶B+树中，结点最多有4个元素，最少有2个元素。

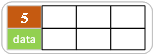
  1. 空树中插入5：

  2. 依次插入8，10，15：

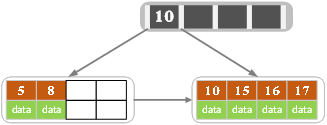
  3. 插入16，

    • 这时超过了关键字的个数限制，所以要进行分裂。在叶子结点分裂时，分裂出来的左节点2个记录，右节点3个记录，中间key成为索引结点中的key，分裂后当前节点指向了父节点（根节点）。结果如下图所示：

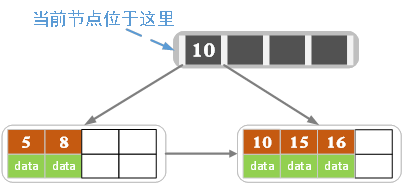
    • 当然我们还有另一种分裂方式，给左结点3个记录，右结点2个记录，此时索引结点中的key就变为15。不同实现而已，本质差不多。

  4. 继续插入17

  5. 插入18，插入后当前节点的关键字个数大于5，进行分裂。

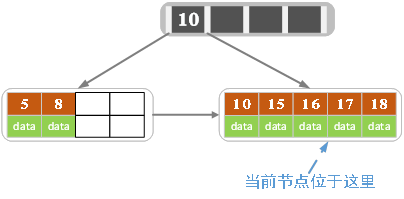
    • 分裂成两个节点，左节点2个记录，右节点3个记录，关键字16进位到父节点（索引类型）中，将当前结点的指针指向父结点。

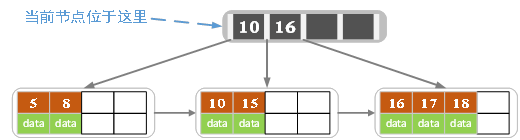
  6. 插入若干数据后：

  7. 在上图中插入7，结果如下图所示

    • 此时当前节点的关键字个数超过4，需要分裂。左节点2个记录，右节点3个记录。分裂后关键字7进入到父节点中，将当前结点的指针指向父节点
    • 当前结点的关键字个数超过4，需要继续分裂。左结点2个关键字，右结点2个关键字，关键字16进入到父结点中，将当前结点指向父结点，结果如下图所示：

2.2 B+树的删除

回顾上文的B树的删除，我们知道B树有元素直删，元素租借，元素合并和元素顶替这四个操作场景，B+树与B树大同小异，几乎没有区别。只不过B+树没有元素顶替

B+树没有元素顶替，是因为B+树的叶子节点，有所有的键值对信息，所以不存在删除的键值对不是叶子节点的情况。

我们下面还是以5阶B+树为例子，在5阶B+树中，结点最多有4个元素，最少有2个元素。

初始状态如下：

  1. 元素直删

    • 在上图基础上删除22
    • 删除后叶子结点中key的个数大于等于2，删除结束

  2. 元素租借

    • 在元素直删完了之后的基础上，再删除15，得到下图：
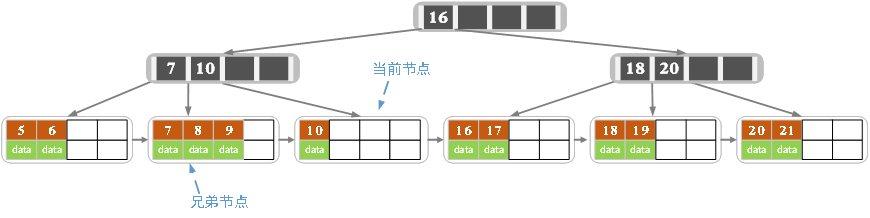
    • 删除后当前结点只有一个元素，不满足条件，而兄弟结点有三个元素（注意，当前节点的兄弟节点只有[7,8,9]），则可以向兄弟节点借一个元素过来。当然，根据排序原则，只能借9。
    • 9元素去到[10]节点之后，那么索引也要相应的更改，否则也不满足排序原则，即原来非叶子节点中的10改为9：

  3. 元素合并

    • 在元素租借完了之后，我们再删除7，删除后的结果如下图所示：
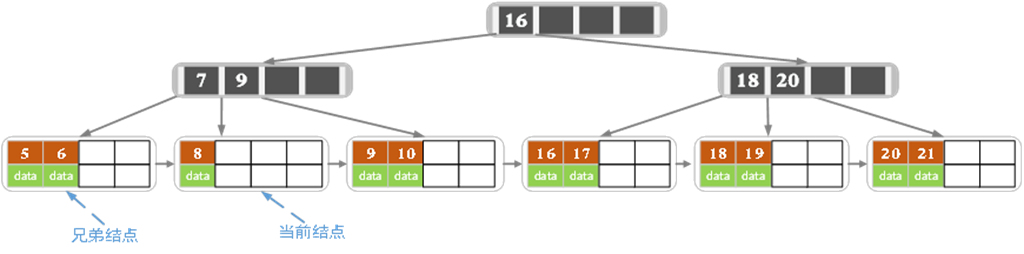
    • 可以看到，删除完了以后，当前节点元素个数小于2，且左右节点的元素数量都是2，即都没有富余的元素。
    • 这时候我们选择元素合并，可以选择和左兄弟合并，也可以和右兄弟合并，这里我们选择左兄弟。
    • 合并的时候我们前文说过，为了保证顺序，兄弟节点还会将父节点中对应的元素一起纳入合并，即[5,6]、[8]会和父节点中的7一起合并，不过这次删除的是7，所以7不存在了，故而，得到：
    • 不过注意，因为7索引的删除，导致了父节点只剩下了一个元素9，这显然不符合数量约束。
    • [9]的兄弟节点也没有余粮，则只能拉着父节点的元素16，和右兄弟[18,20]合并。得到下图：

其实说是没有元素顶替，但为了便于理解，也可以用元素顶替的思路来看最后这个删除操作：
1.因为删除的是7，7也在非叶子节点上，所以7删除了，要从子节点中找一个元素来顶替。
2.不论是8顶替上去还是6顶替上去，都会使得有个子节点数量不符合，触发元素合并。
3.这时候左右节点的元素+他们关联的父节点的元素合并，得到的结果，还是[5,6,8]

2.3 B+树的优点

  1. B+树的层级更少：相较于B树，B+每个非叶子节点存储的元素数更多（因为B+树的非叶子节点不存data，相同容量下可容纳的元素更多），使得B+树相对于B树更加“矮胖”，即B+树的层级更少所以查询数据更快；

  2. B+树查询速度更稳定：B+所有关键字数据地址都存在叶子节点上，所以每次查找的次数都相同所以查询速度要比B树更稳定。不像B树，有时候在非叶子节点上找到，那就相对快，有时候在叶子节点上找到，那就相对慢。

  3. B+树天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在查询大小区间的数据时候更方便，数据紧密性很高，缓存的命中率也会比B树高。

  4. B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

2.4 为什么B+树比B树更适合做数据库索引？

其实理由也正是基于上诉的优势而言，不过我们把语义按照数据库索引适配性的角度转化一下：

  1. B+树的磁盘读写代价更低：B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。

  2. B+树的查询效率更加稳定：由于非叶节点并不是最终指向文件内容的节点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根节点到叶子节点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

  3. 对范围查询的适配性好：在数据库中基于范围的查询是非常频繁的，B树不支持这样的操作或者说效率太低。而B+树只需要去遍历叶子节点的链表，就可以实现整棵树的范围查询。

  4. 全节点遍历更快：由于B+树的数据都存储在叶子节点中，分支节点均为索引，方便扫库，只需要扫一遍叶子节点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引。

0%