前言
在正文开始前,我们先来了解一下有向无环图(Directed Acyclic Graph简称DAG)
如下图就是一个DAG图,DAG图是我们讨论拓扑排序的基础。
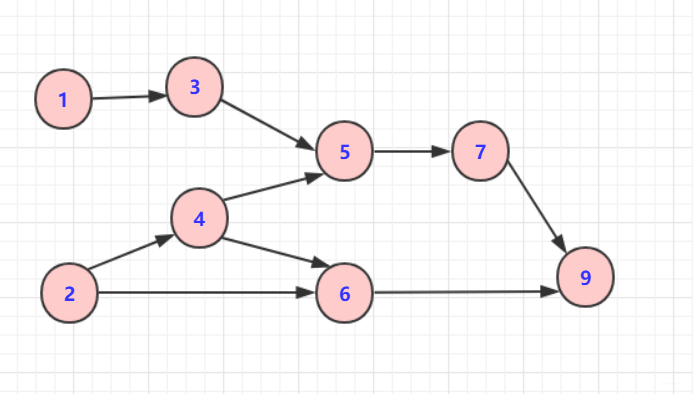
AOV网:数据在顶点 可以理解为面向对象
AOE网:数据在边上,可以理解为面向过程!
1. 什么是拓扑排序
拓扑排序(Topological Order),很多人听说过,但是不了解的一种算法。或许很多人只知道它是图论的一种排序,至于干什么的不清楚。又或许很多人可能还会认为它是一种啥排序。
而实质上它只是将DAG图的顶点排成一个线性序列,得到一个顶点的全序集合。其排序的顺序依据就是节点的指向关系。比如前言的DAG图:
- …
- 节点5在节点4和节点3的后面
- 节点9在节点6和节点7的后面
- …
那么最后得到的节点的线性序列结果,也一定要满足上面的指向顺序。
每一个节点都拥有入度(有多少点导向它,也就是开始它有多少前提)和出度(它导向多少点,也就是它是多少其他节点开始的前提)。例如节点5的入度为3和4,出度为7。
拓扑排序的结果不是唯一的,只要符合上面的条件,那么它就是拓扑序列,比如1 2 4 3 6 5 7 9和2 1 3 4 5 6 7 9,这两个结果都是可行的。
官方一点的定义:将有向图中的节点以线性方式进行排序。即对于任何连接自节点u到节点v的有向边uv,在最后的排序结果中,节点u总是在节点v的前面。
2. 现实案例
看了上面关于拓扑排序的概念如果还觉得十分抽象的话,那么不妨考虑一个非常非常经典的例子——选课。
假设我非常想学习一门《jsp入门》的课程,但是在修这么课程之前,我们必须要学习一些基础课程,比如《JAVA语言程序设计》,《HTML指南》等等。那么这个制定选修课程顺序的过程,实际上就是一个拓扑排序的过程,每门课程相当于有向图中的一个顶点,而连接顶点之间的有向边就是课程学习的先后关系。
只不过这个过程不是那么复杂,从而很自然的在我们的大脑中完成了。将这个过程以算法的形式描述出来的结果,就是拓扑排序。
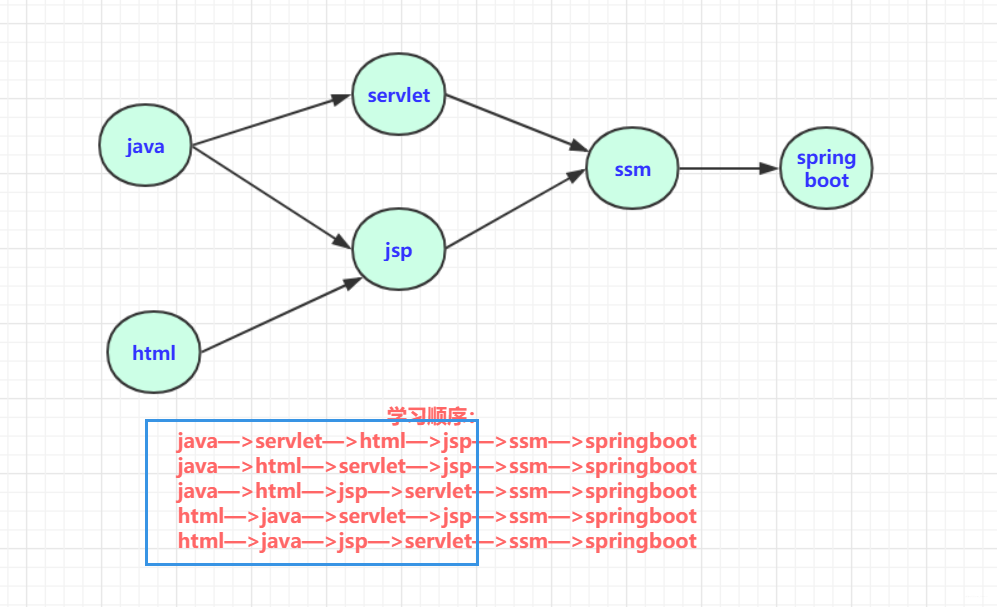
可以看到,上图中的学习顺序,就是拓扑序列,其不止一个结果。
拓扑排序算法在工程学中十分重要。
节点成环的图,无法被拓扑排序,因为这在工程上本身没有意义,比如A——>B——>C——>A,那么这个工程永远无法被开始。
3. 算法实现
拓扑排序的最优时间复杂度是O(m+n),其中m和n是DAG图中节点数和边数。因为拓扑排序至少要对DAG图的节点和边进行一次完整的遍历。
拓扑排序的最优空间复杂度是O(m+n),其中m和n是DAG图中节点数和边数。我们一般使用邻接表来存储DAG图,因此空间复杂度是O(m+n)。
3.1 广度优先搜索法(BFS)
3.1.1 BFS实现拓扑排序
广度优先搜索法的思路很简单:
- 从DAG图中找到入度为0的节点A(也就是没有箭头指向它的节点),将其放入拓扑序列的结果集。
- 同时删除由节点A出发的所有边。
- 在剩下的DAG图中重复1-2两步。
- 如果最后可以把全部的节点都删除并加入到结果集,那表示DAG图可以被拓扑排序;否则,如果最后有节点被剩下,那说明该图是有环图,无法被拓扑排序。
如下图

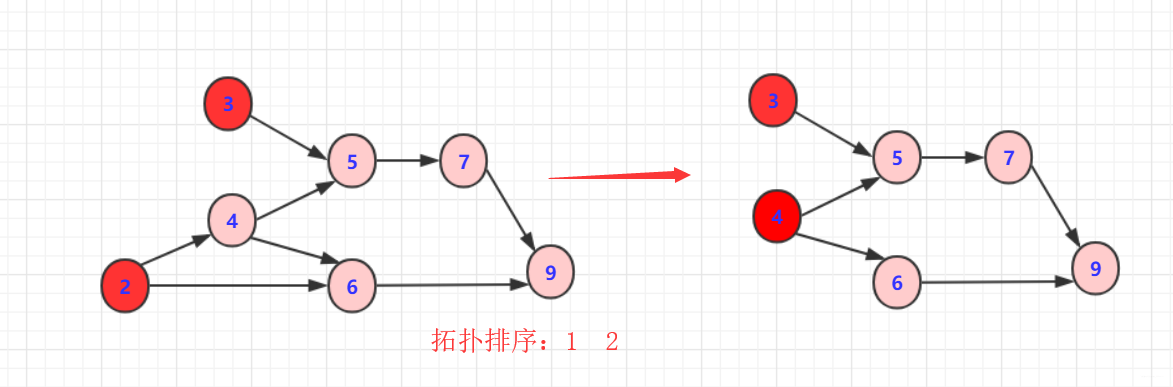
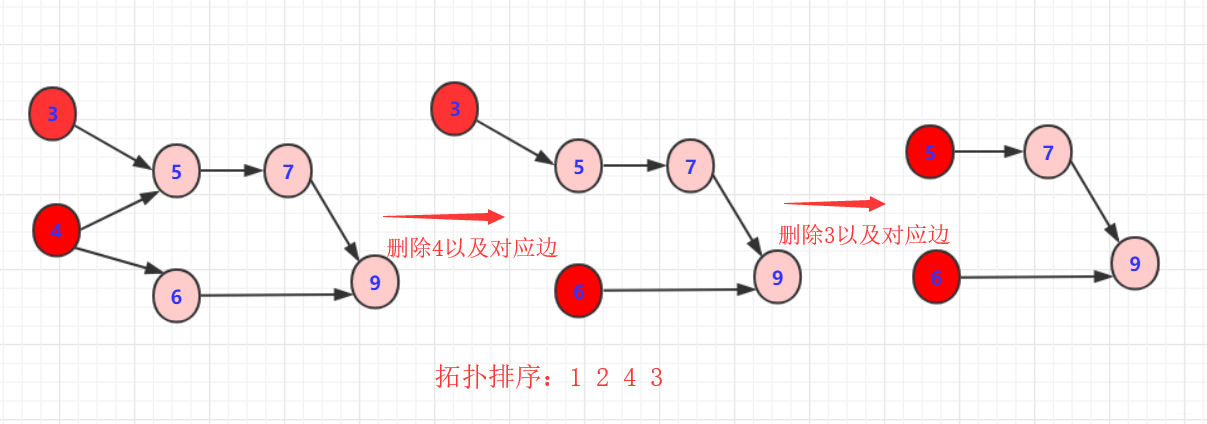
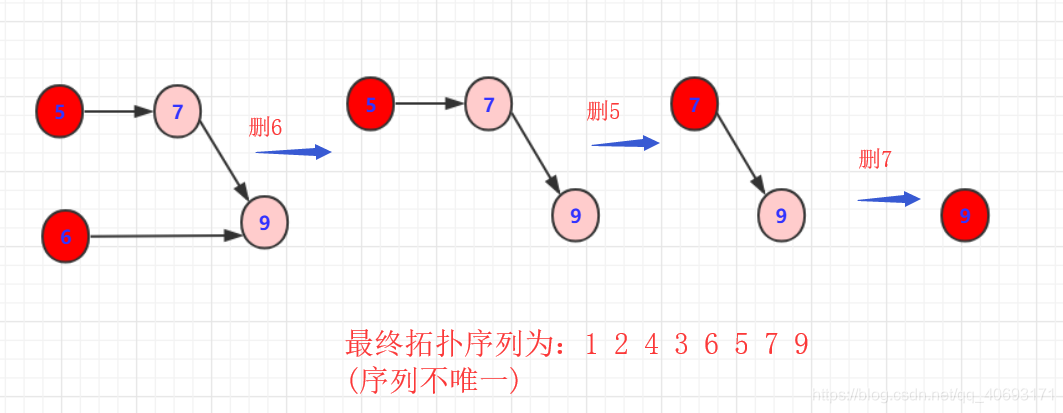
3.1.2 BFS实现拓扑排序的优化
如果有时候,我们只需要知道某个DAG图是否可以拓扑排序,而不需要真正得到拓扑排序后的结果,那么可以不需要结果集列表,只需要统计被删除的节点的数量即可,如果该数量等于DAG图的节点数,那么DAG图可以被拓扑排序。
3.2 深度优先搜索法(DFS)
3.2.1 DFS实现拓扑排序
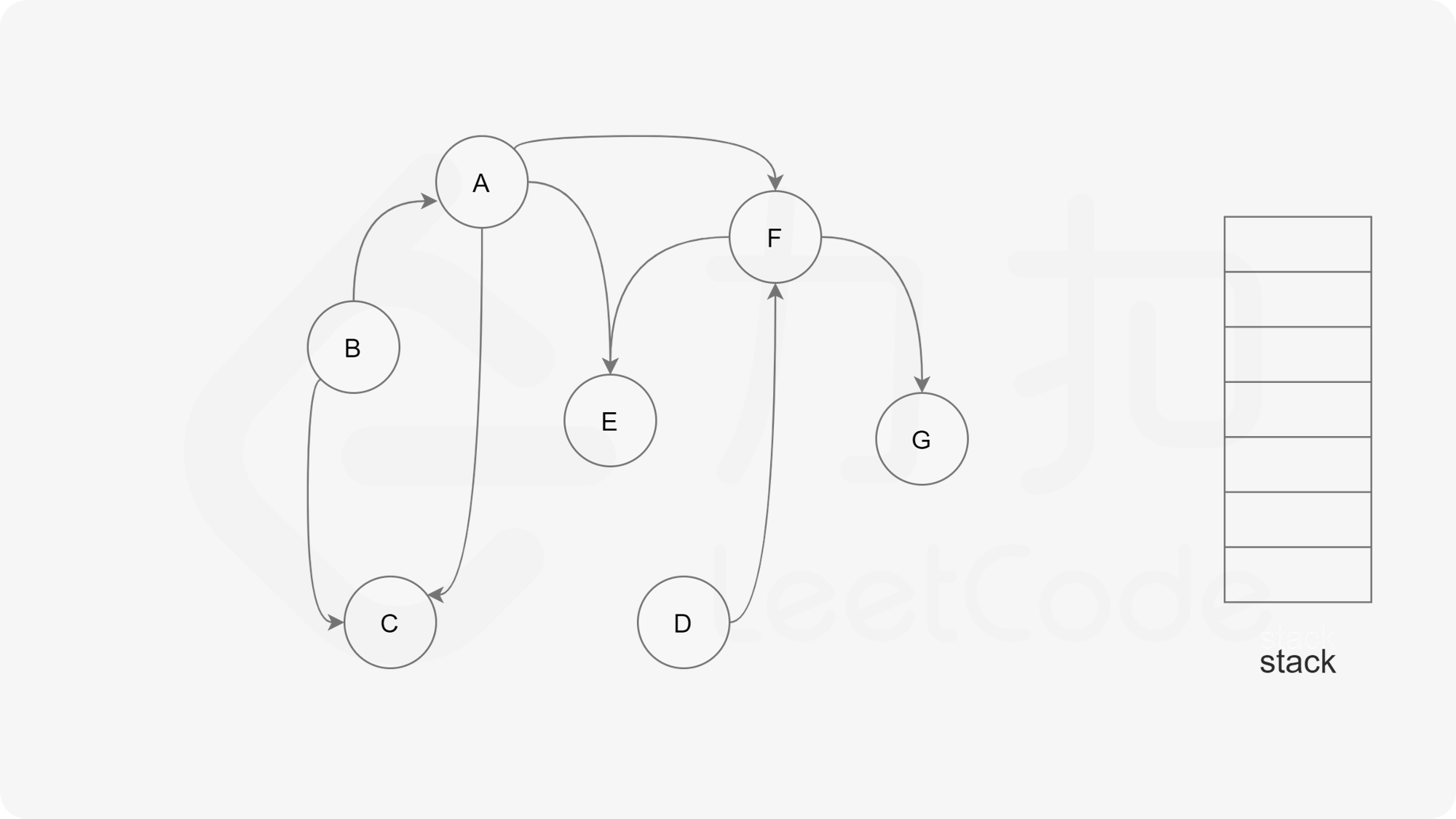
深度优先搜索法是广度优先搜索法的逆向思路,它的步骤如下:
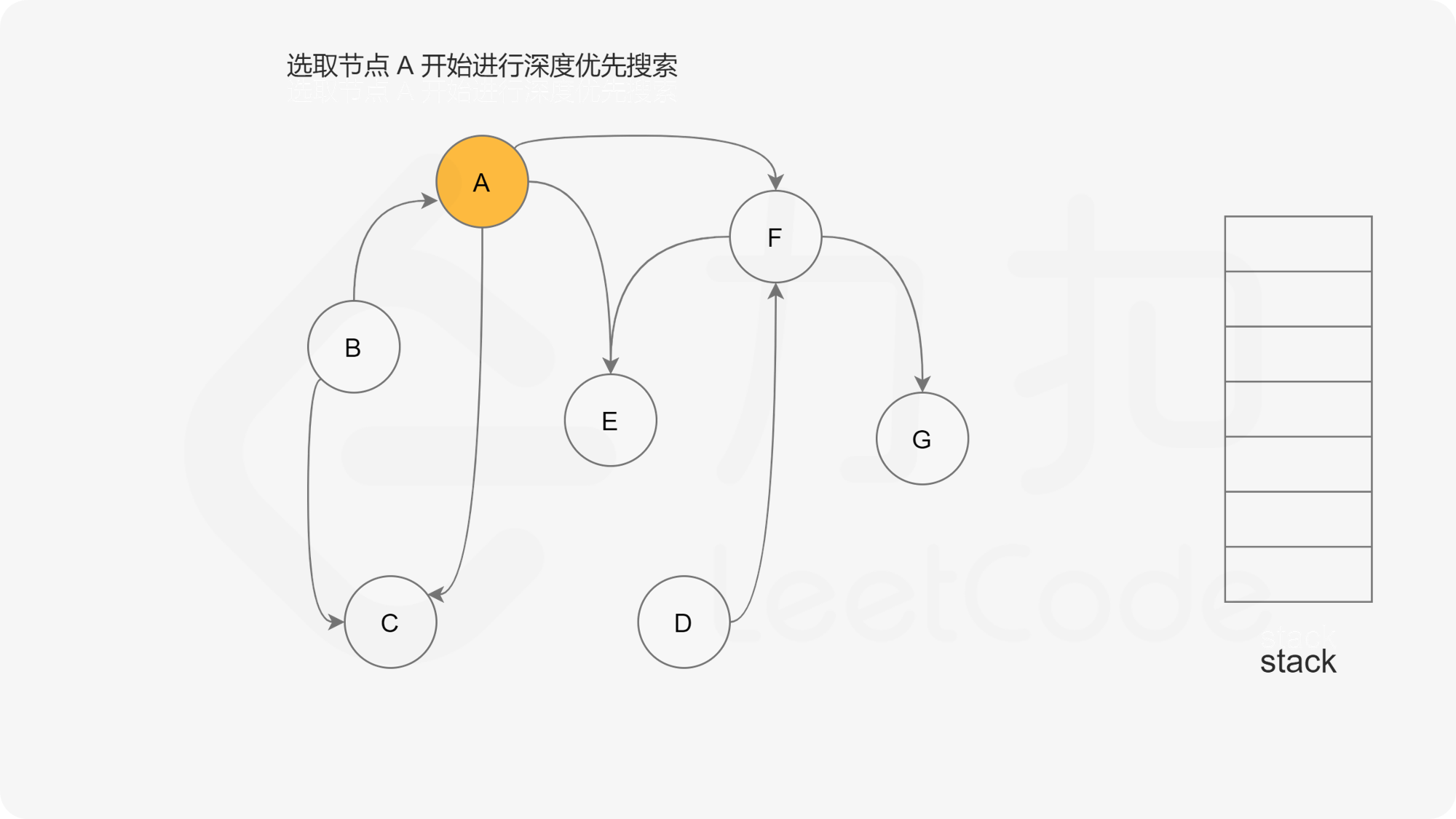
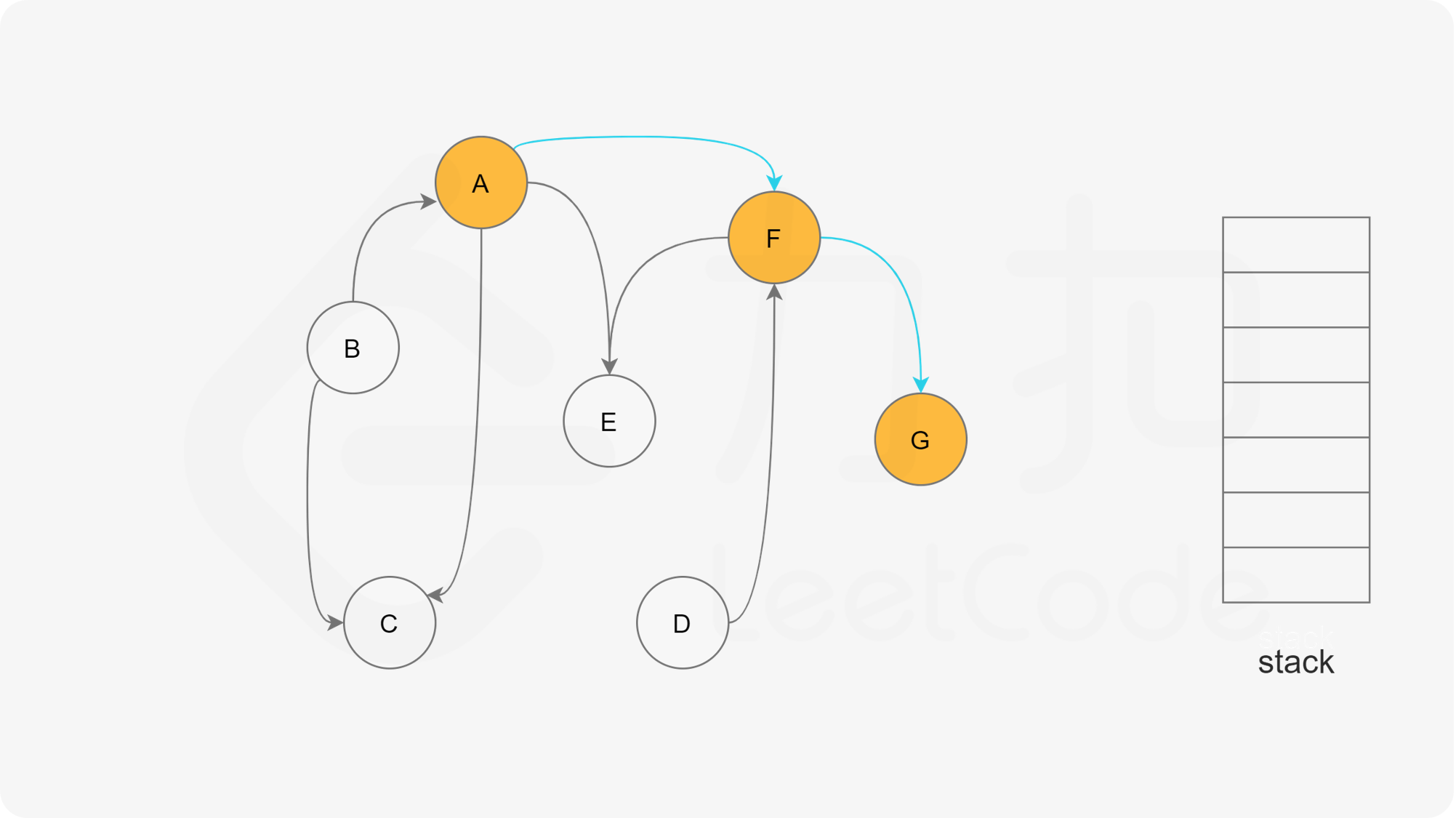
- 选取图中任意一个节点A,将其状态标记为“搜索中”
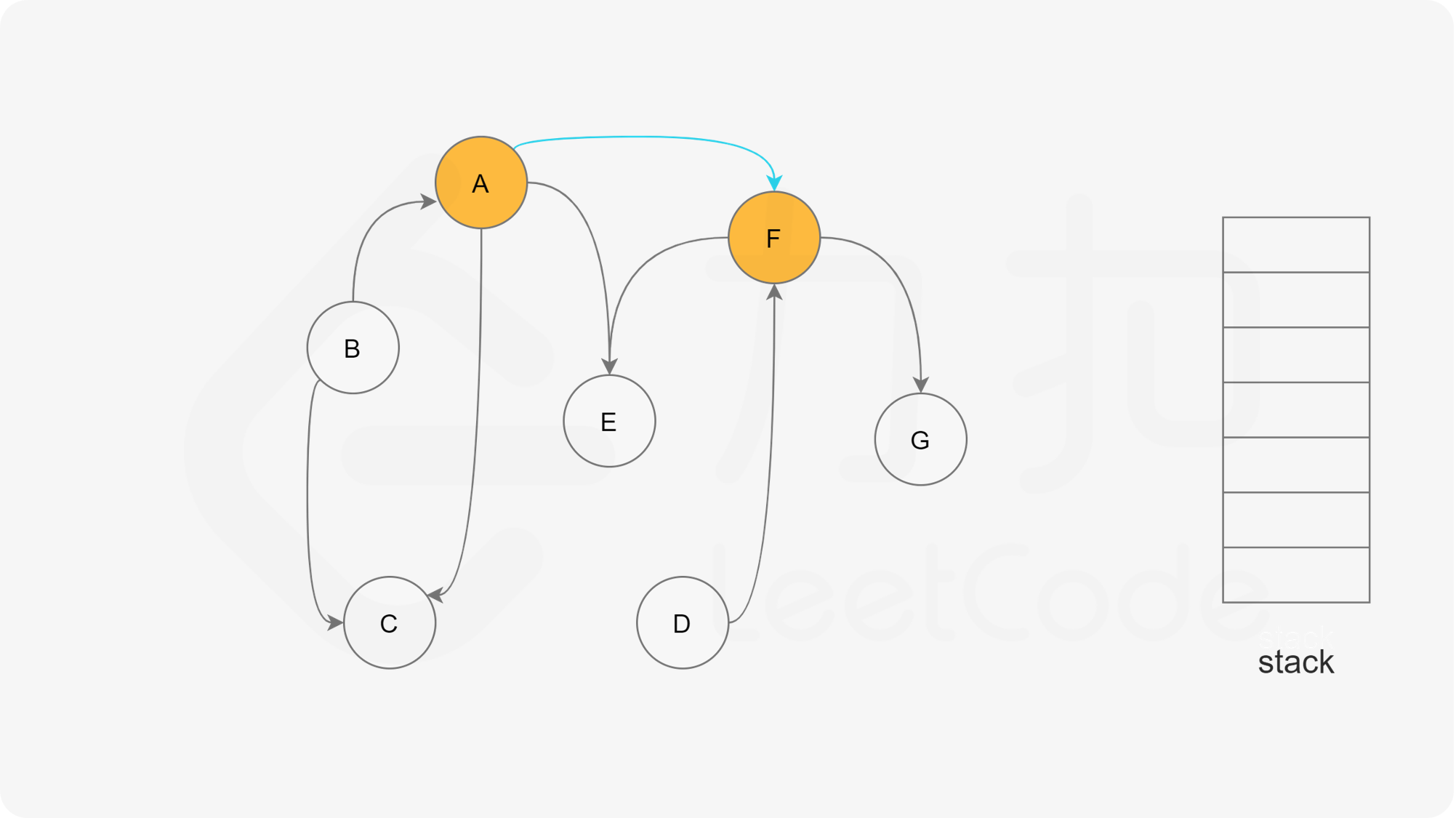
- 寻找节点A的邻接点(沿着箭头指向寻找相邻的节点)
- 如果A存在邻接点
- 如果A的邻接点中存在状态为“搜索中”的邻接点,那么表示DAG图有环路,不可拓扑排序。
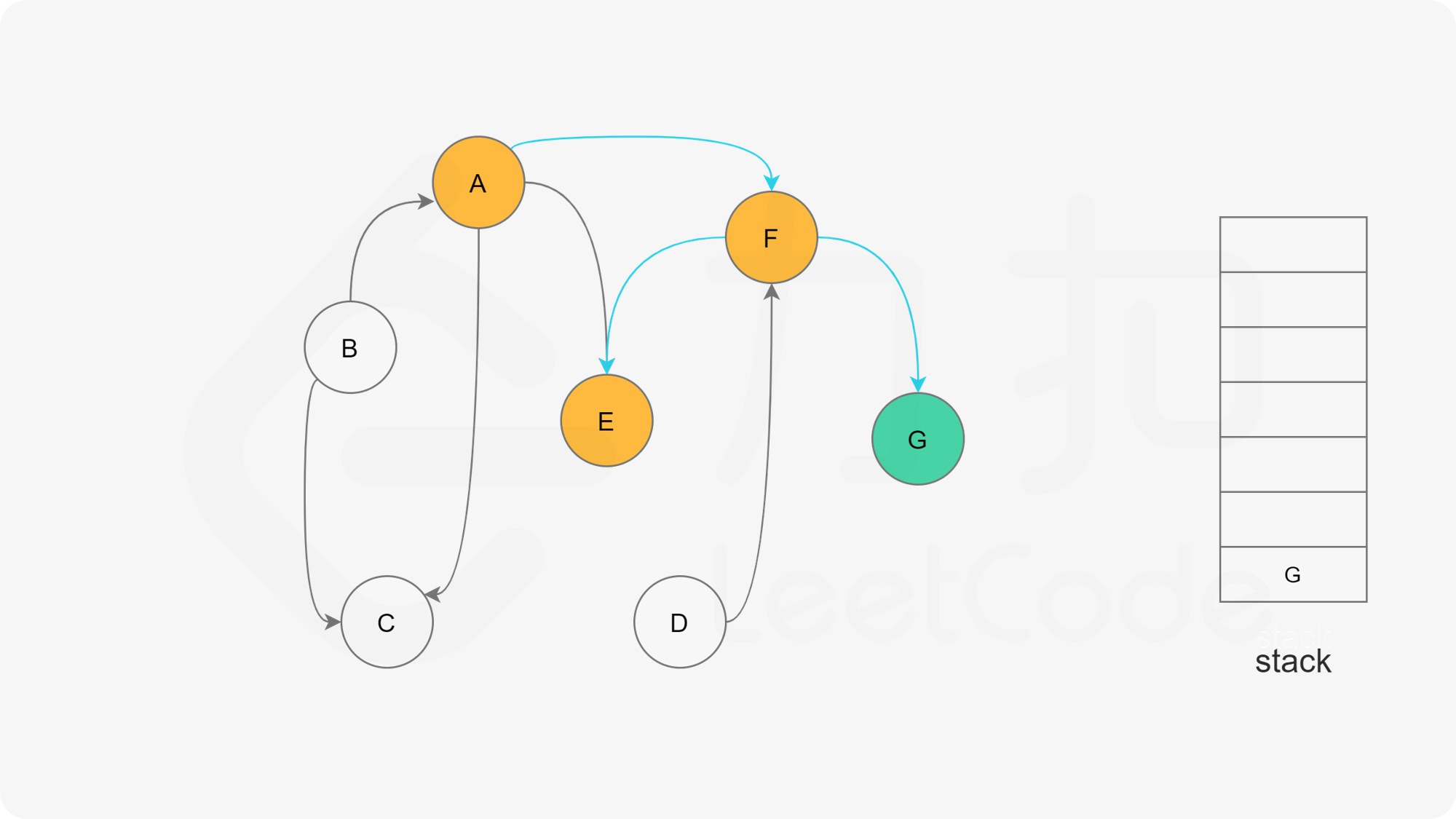
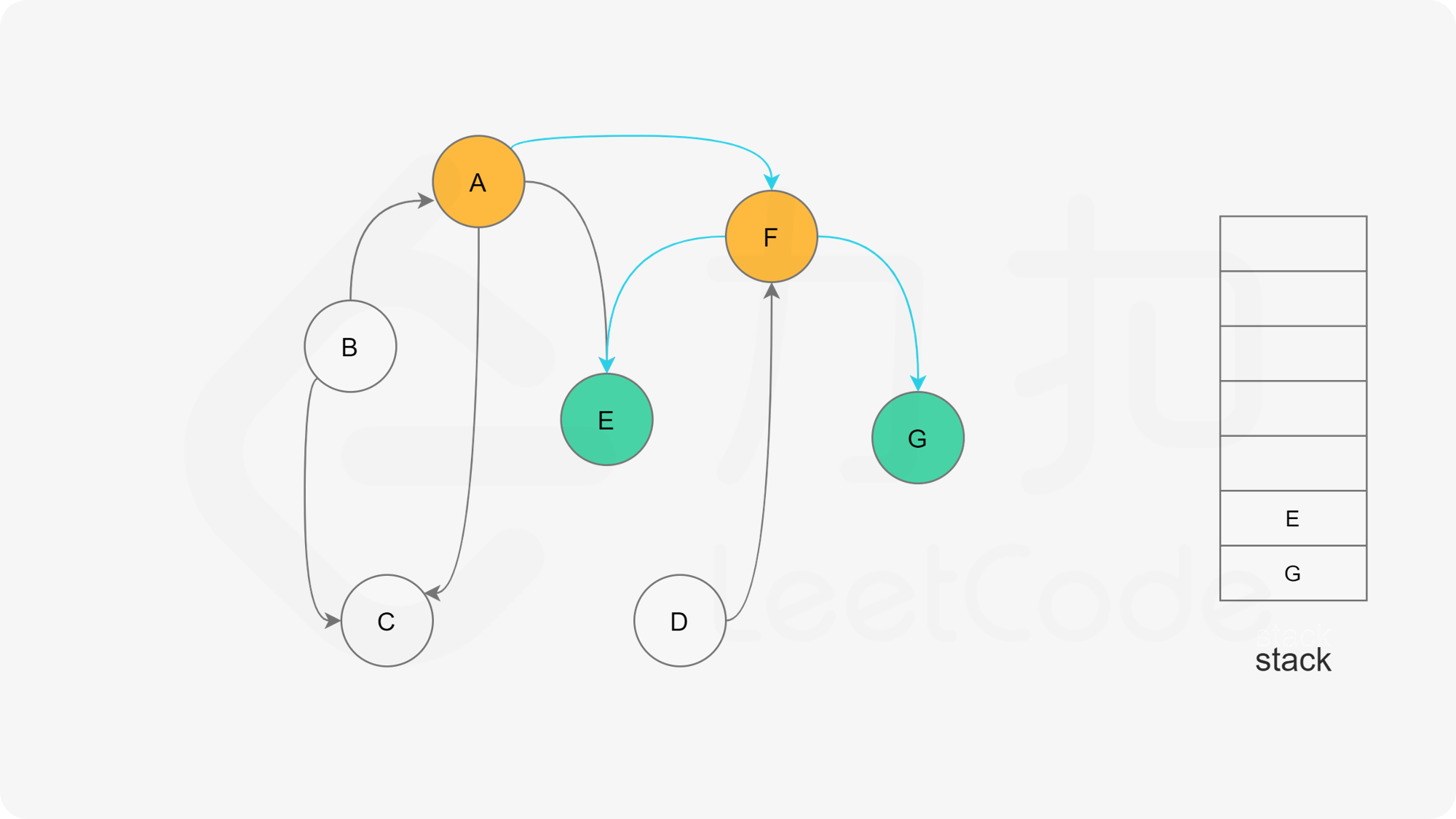
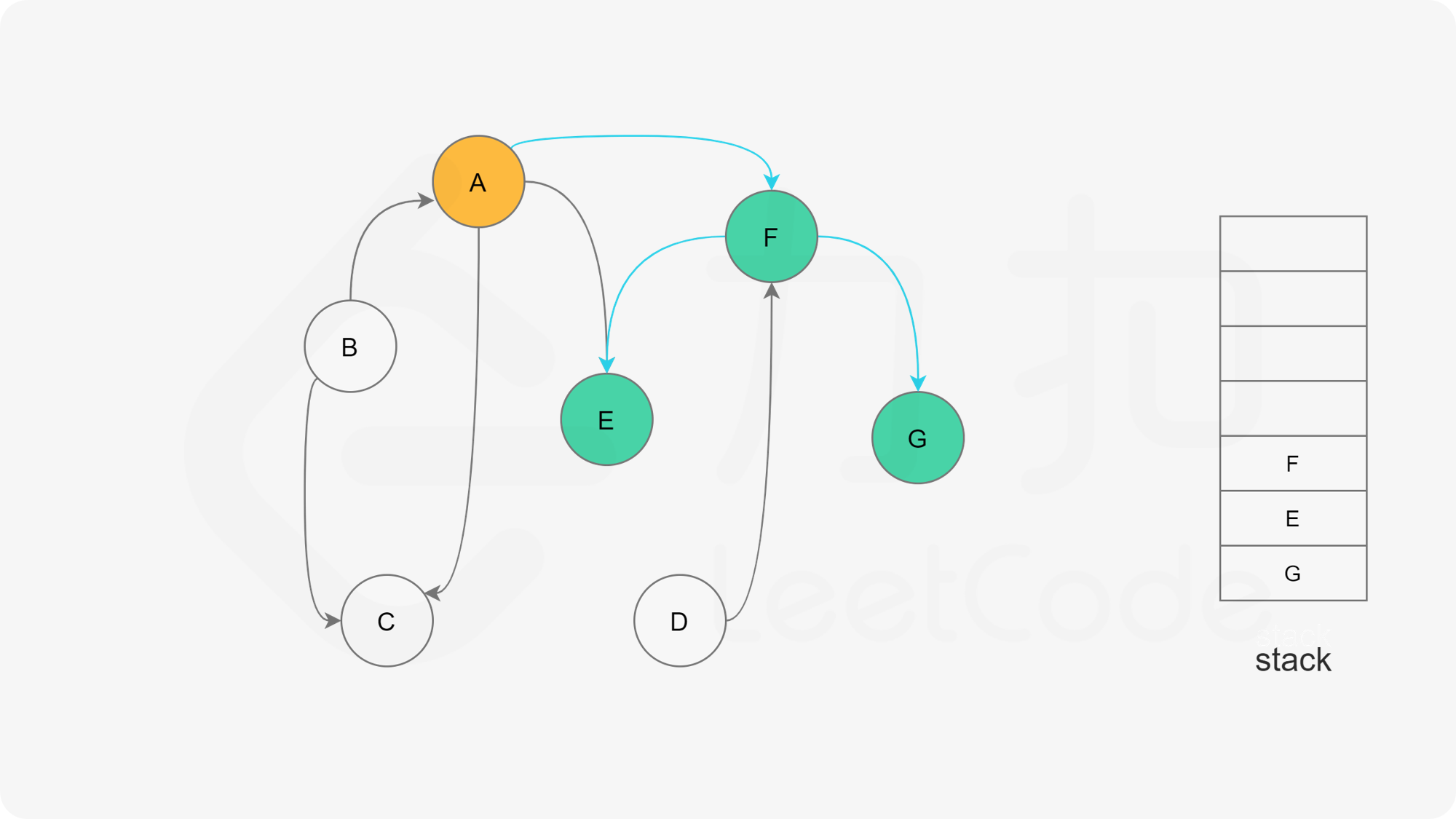
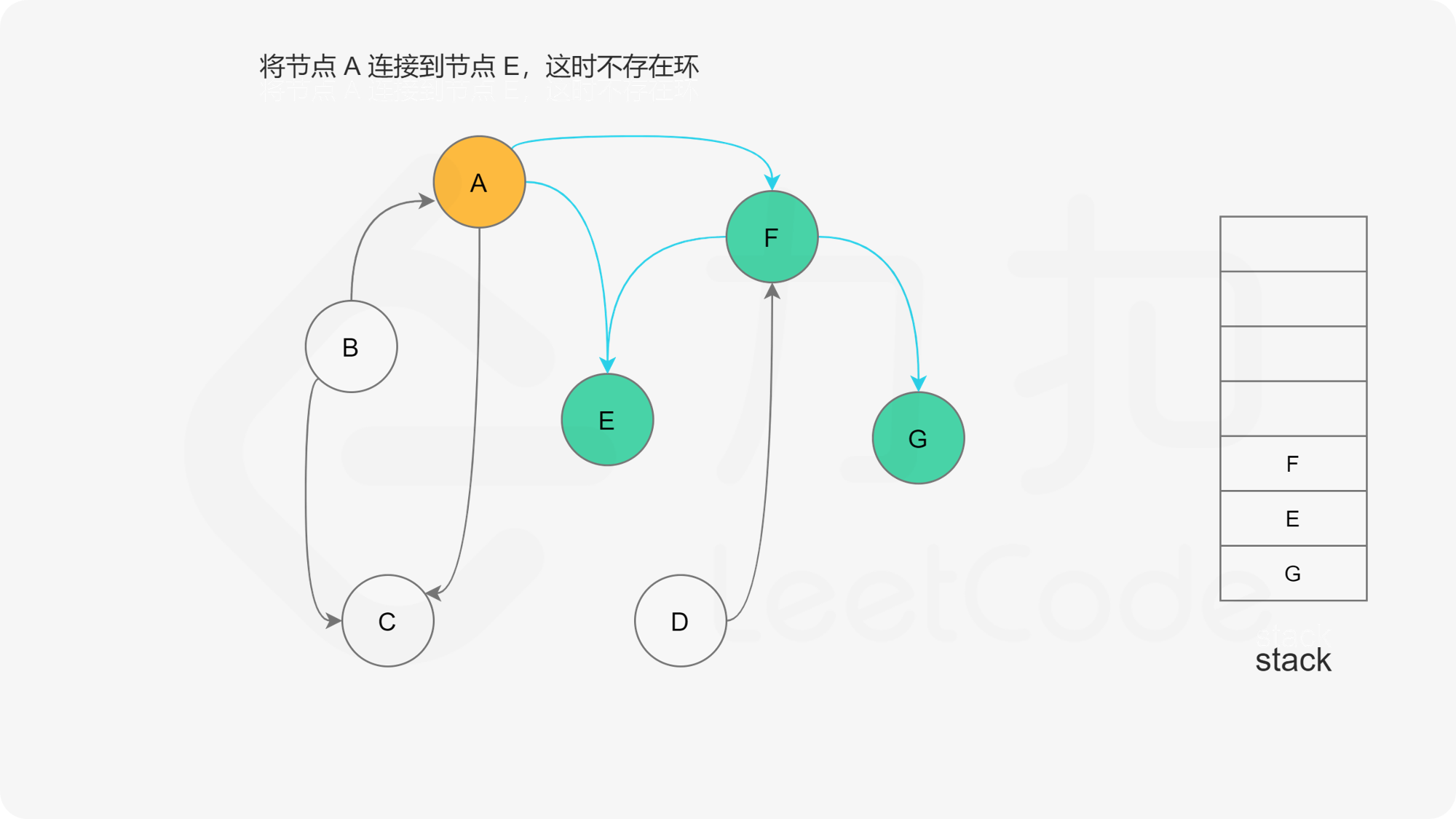
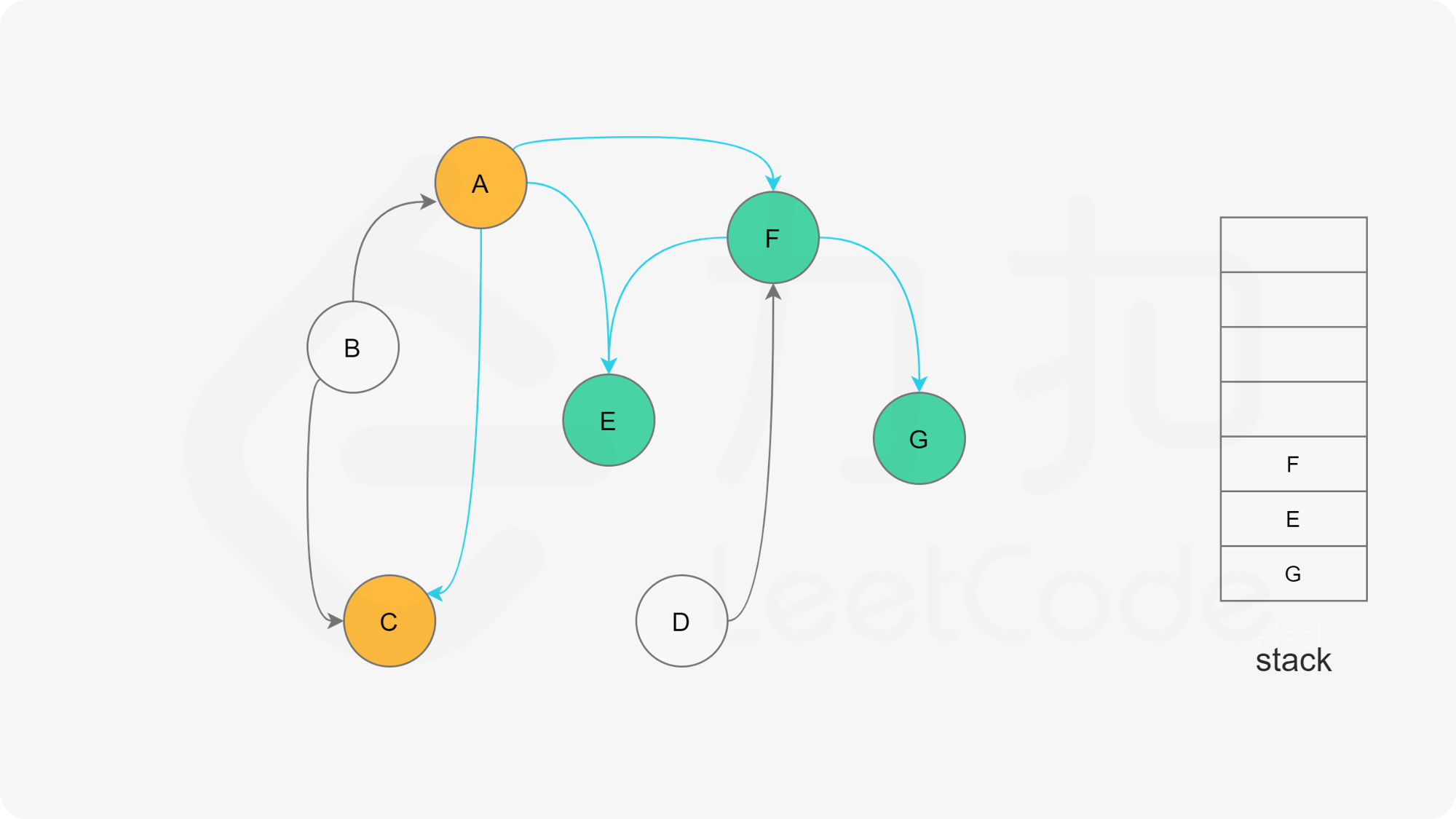
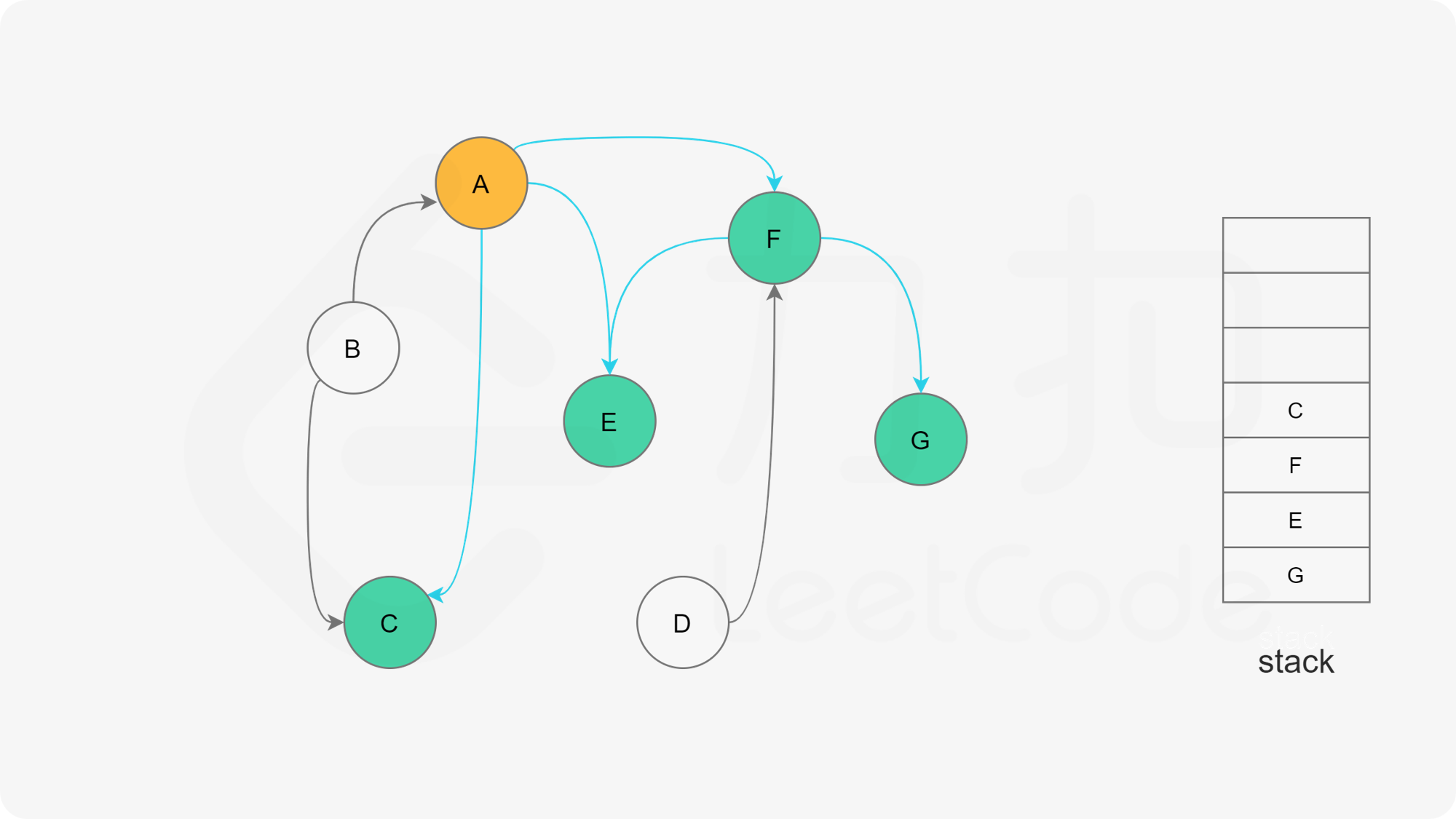
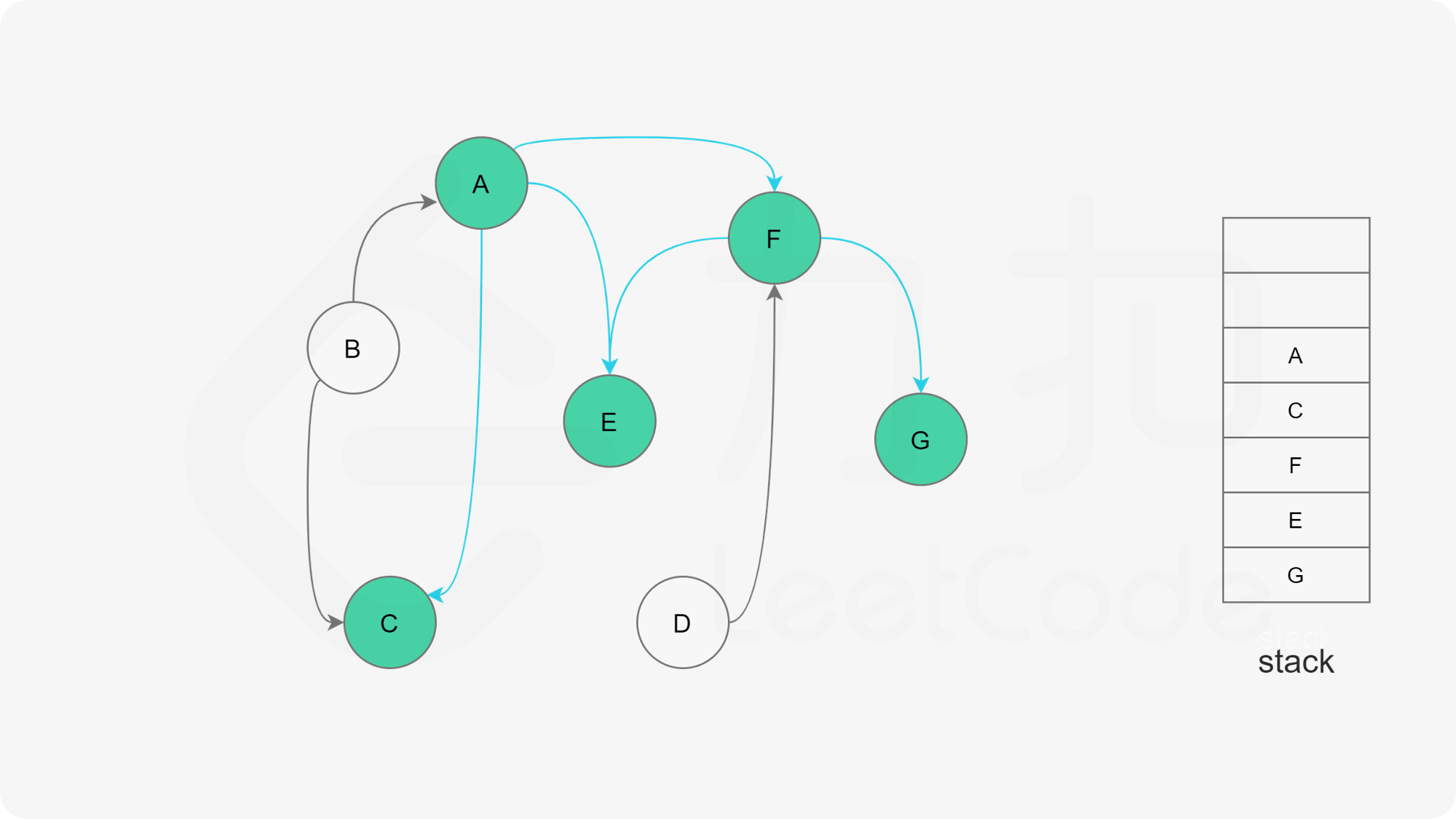
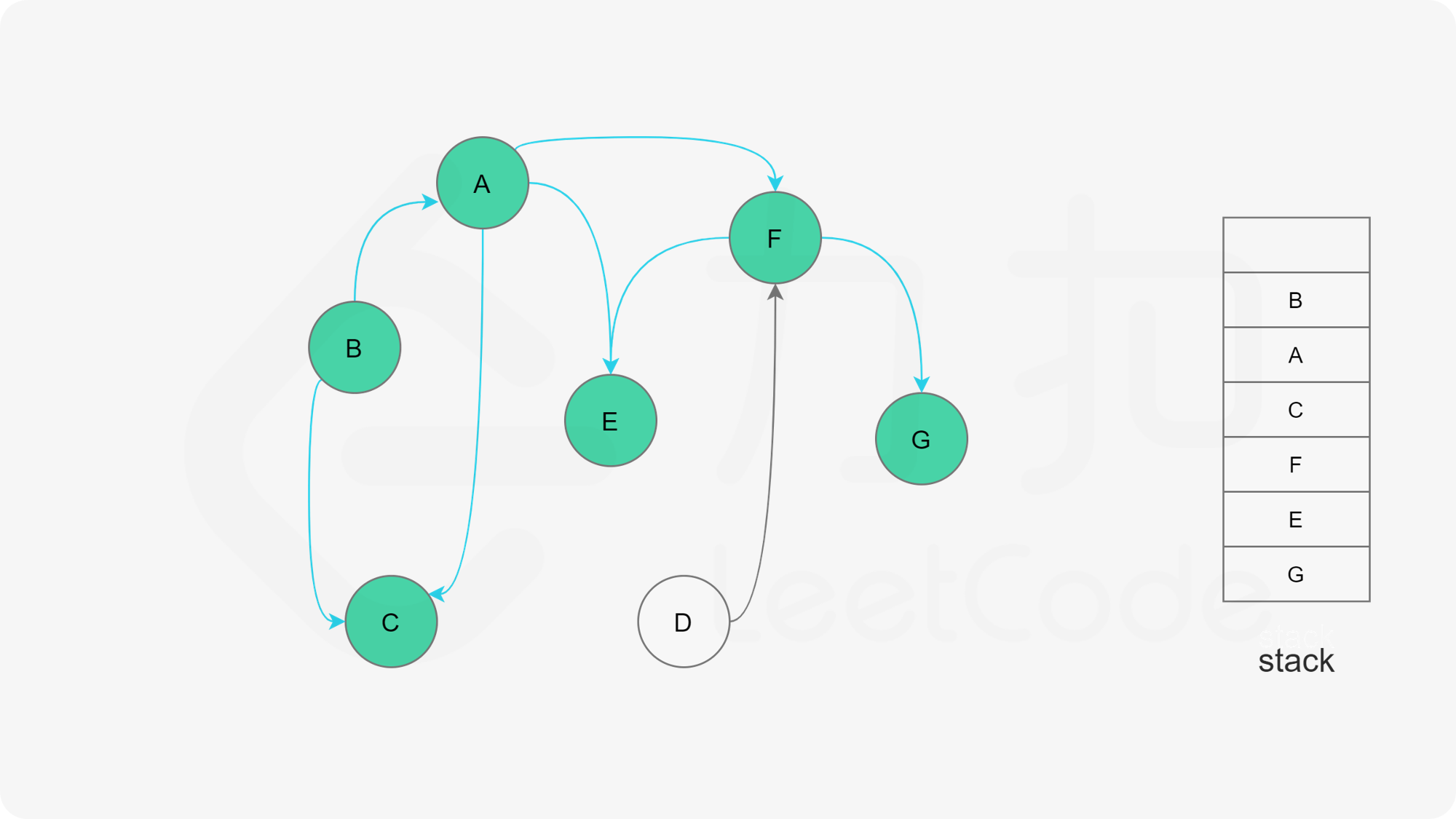
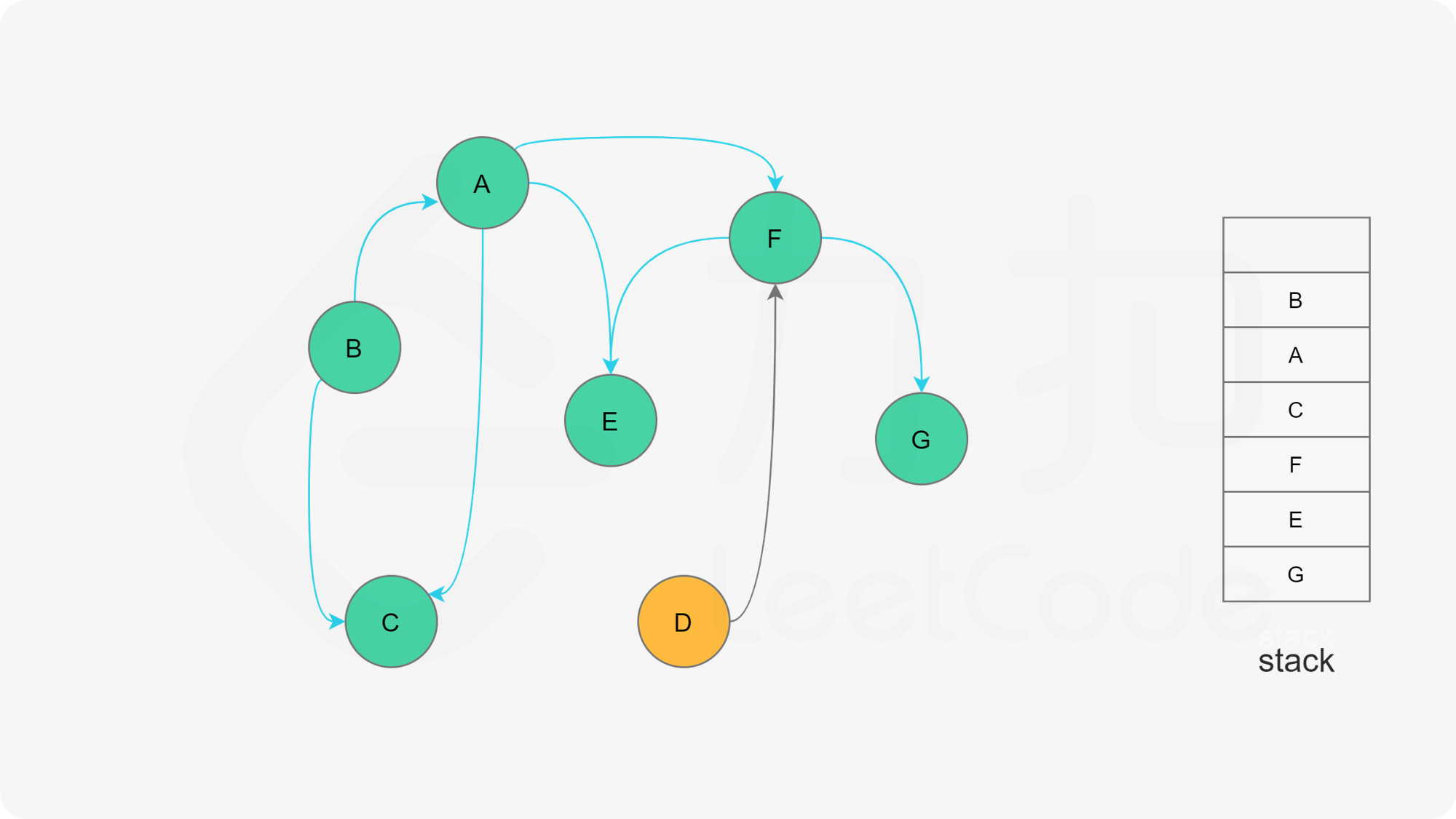
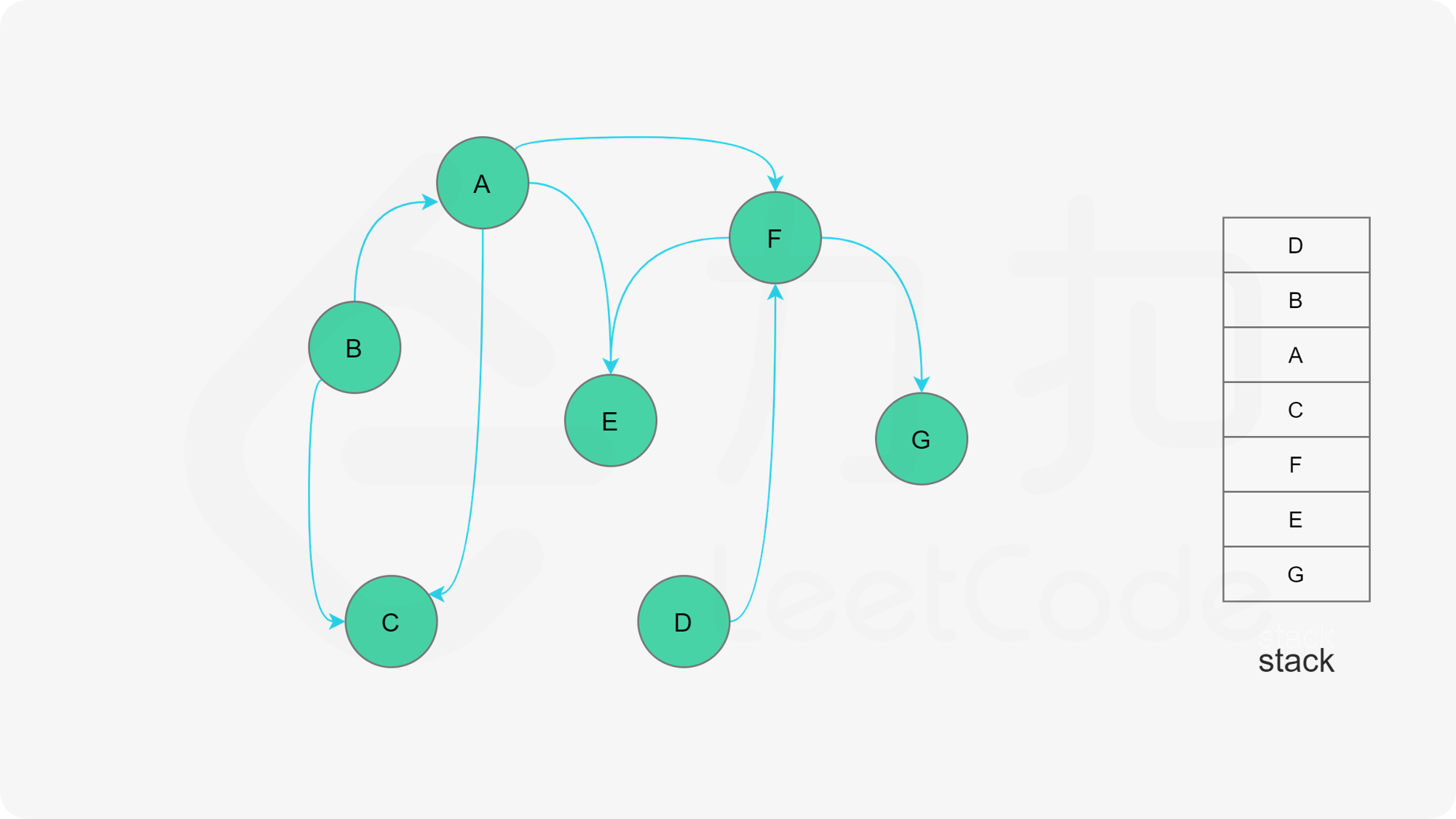
- 否则,那么任意选择一个状态为“未搜索”的邻接点B,使用递归对B重复做1和2操作,注意此时B的邻接点判断不包含来路(也就是A节点)。等到A的所有邻接点都被搜索到,递归回溯回A节点的时候,那么A节点也会被标记为“已搜索”,并压入结果栈。
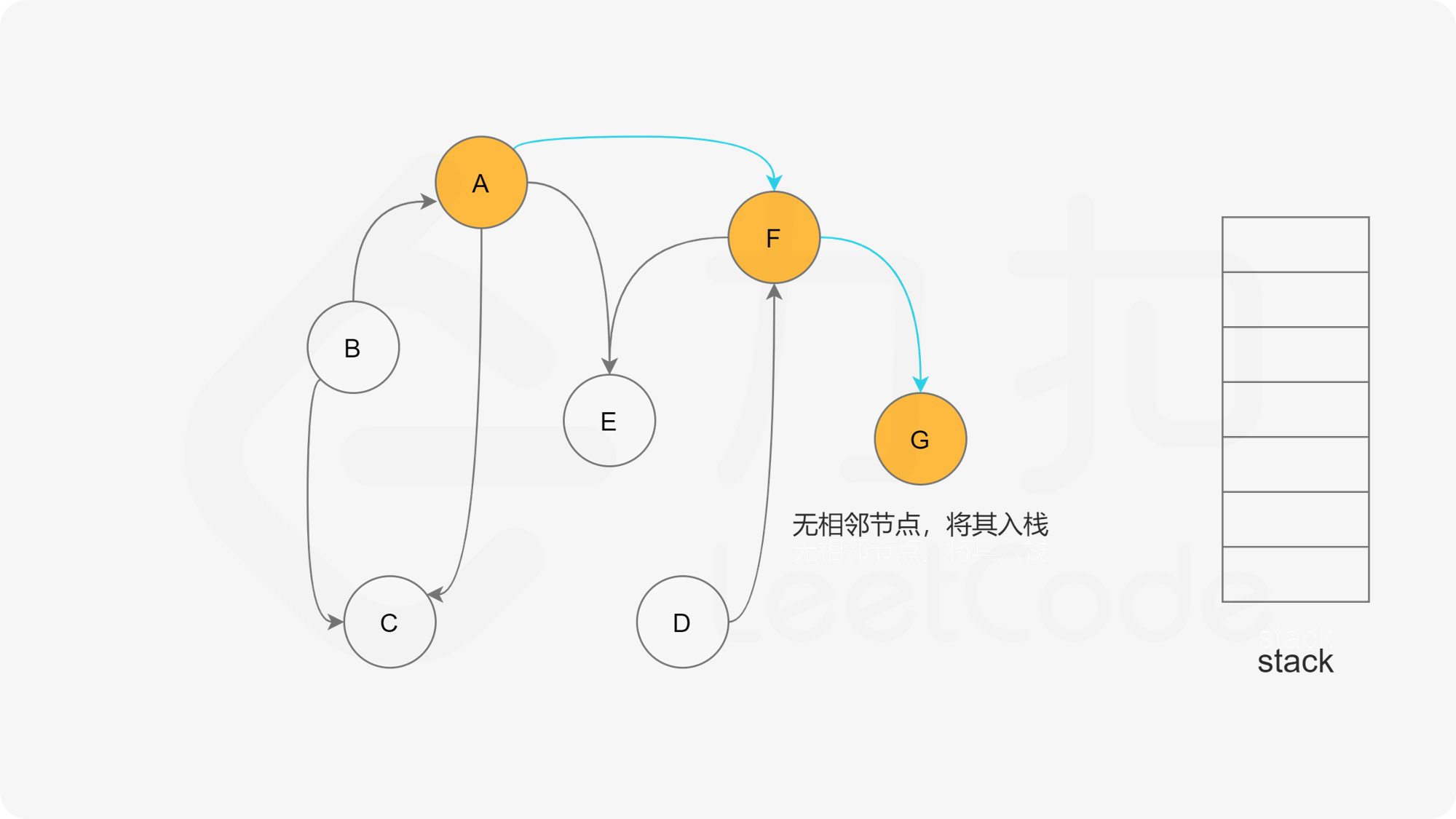
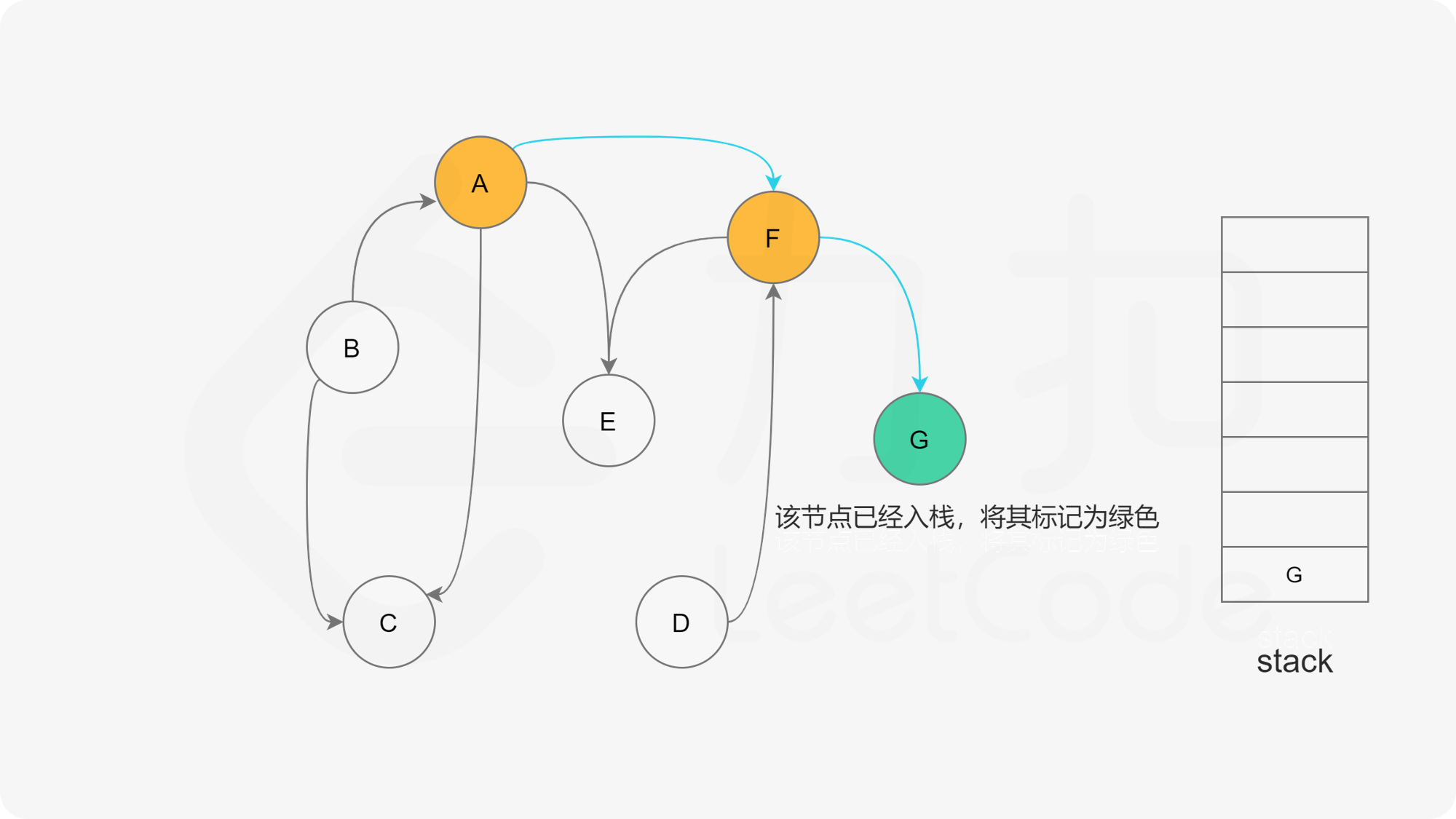
- 如果A不存在邻接点,那么将节点A的状态改为“已完成”,并且将其压入一个结果集的栈中。
- 如果A存在邻接点
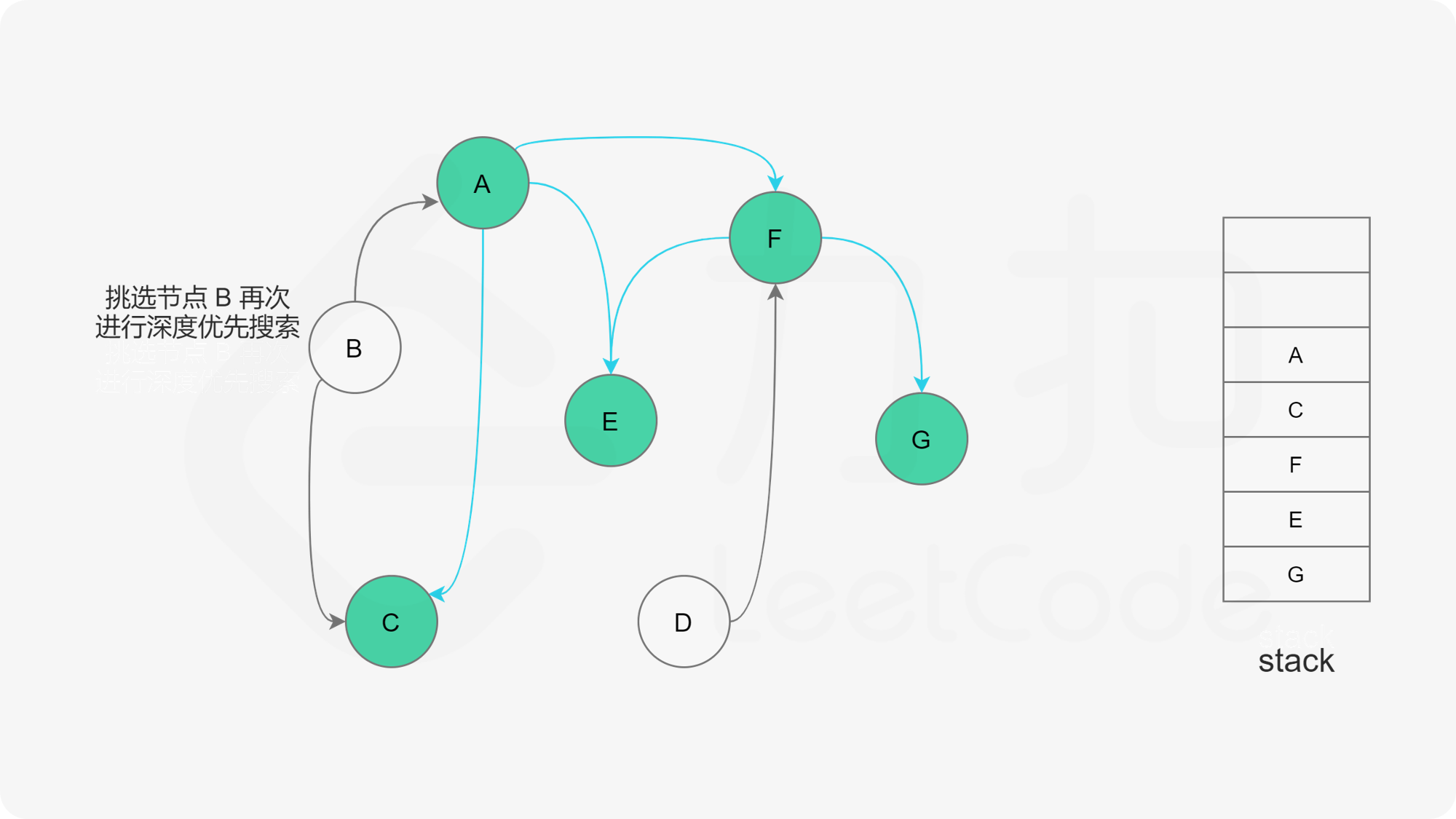
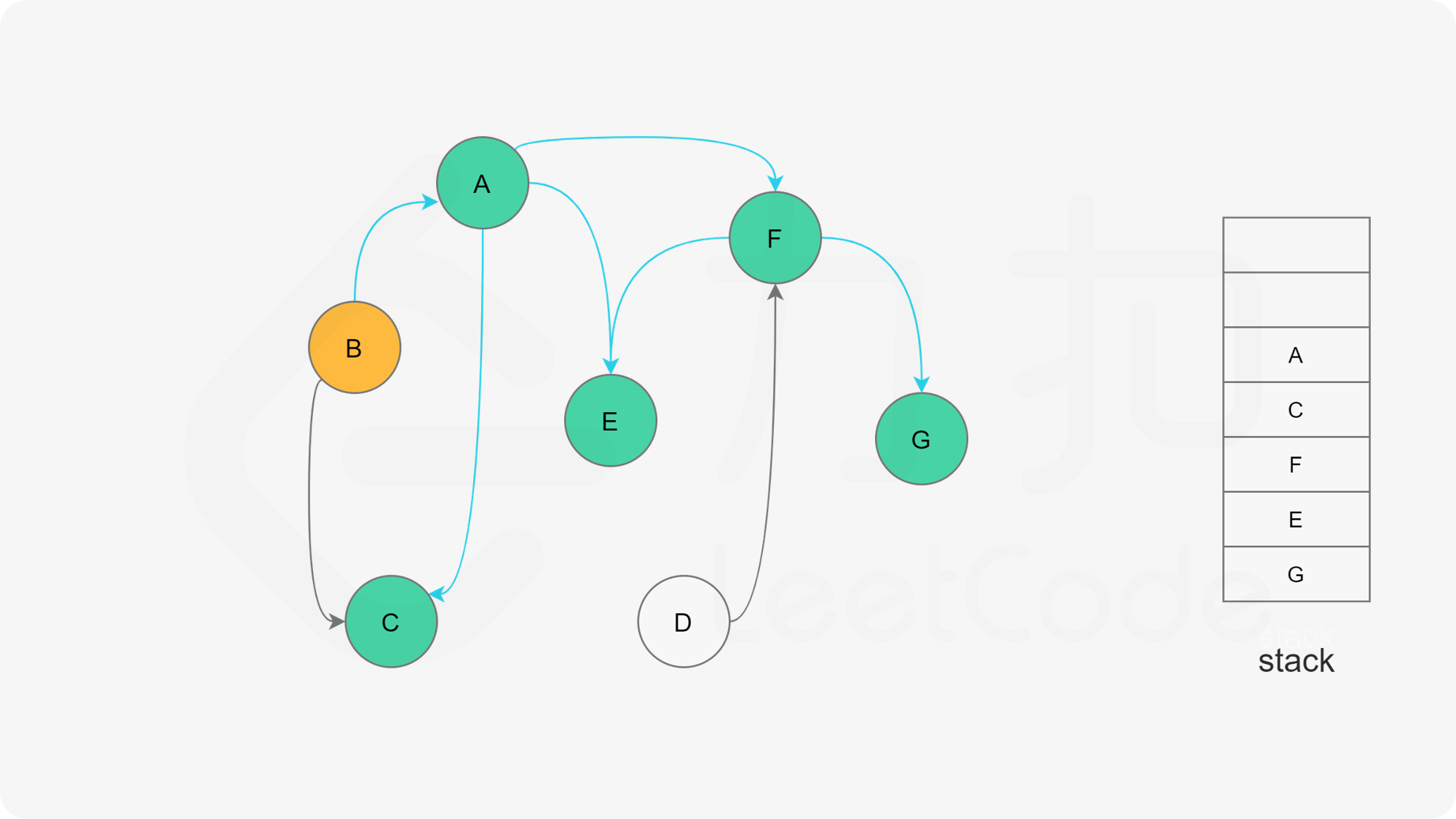
- A节点及其相邻节点都搜索完毕后,如果还有未搜索的节点,那么任意选取一个节点当做出发点,继续重复1,2,3步骤。
- 直到所有的节点都被搜索并压入栈,那么此时结果栈中,从栈顶到栈底的顺序,就是拓扑排序的顺序。
3.2.2 DFS实现拓扑排序的优化
如果有时候,我们只需要知道某个DAG图是否可以拓扑排序,而不需要真正得到拓扑排序后的结果,那么可以不需要结果栈,只需要判断整个深度优先搜索过程,没有发生“搜索中”节点的相邻节点(不包含来路的节点)也是“搜索中”就行。