前言

在JAVA开发中，我们经常需要操作数组和集合，其中数组和链表的排序是重中之重。

Arrays.sort方法用来对数组排序。Collections.sort()方法用来对链表排序，而Collections.sort()的底层，其实使用的也是Arrays.sort方法。

所以JAVA内置排序的核心类，都在于Arrays工具类，接下来我们也重点剖析该类。

1. Arrays工具类

我们先来看下Arrays工具类对外暴露的sort方法列表。

A：从排序范围角度划分，sort方法分为了

针对数组的整体做排序的方法，如
- sort(int[] a)
- sort(Object[] a)
- sort(T[] a, Comparator<? super T> c)
针对数组的局部做排序的方法，如
- sort(int[] a, int fromIndex, int toIndex)
- sort(Object[] a , int fromIndex, int toIndex)
- sort(T[] a, int fromIndex, int toIndex,Comparator<? super T> c)

B：从排序类型角度划分，sort方法分为了

对数组按照默认升序的方式进行排序的方法，如
- sort(int[] a)
- sort(Object[] a)
- sort(int[] a, int fromIndex, int toIndex)
- sort(Object[] a , int fromIndex, int toIndex)
对数组按照自定义排序类型进行排序的方法，如
- sort(T[] a, Comparator<? super T> c)
- sort(T[] a, int fromIndex, int toIndex,Comparator<? super T> c)

C：从操作对象角度划分，sort方法分为了

对基本类型（byte，int，char等）数组操作的方法
- sort(int[] a)
- sort(int[] a, int fromIndex, int toIndex)
对对象类型（object）数组操作的方法
- sort(Object[] a)
- sort(Object[] a , int fromIndex, int toIndex)
- sort(T[] a, Comparator<? super T> c)
- sort(T[] a, int fromIndex, int toIndex,Comparator<? super T> c)

这里最重要的划分是C：从操作对象角度划分，因为JAVA对不同类型的数组，定义了不同的实现方法（以常用的JDK 1.8版本为例），我们先来开门见山的总结一下：

2. 基本类型数组的排序

对于基本数据类型的数组，假设数组长度为length：

如果length<47，那么采用插入排序算法。
如果47<=length<286，或者286<=length，但数组不具备特定结构，那么使用快速排序的一种优化形式：双轴快排算法。
如果286<=length，并且数组具备特定结构，那么使用归并排序算法。

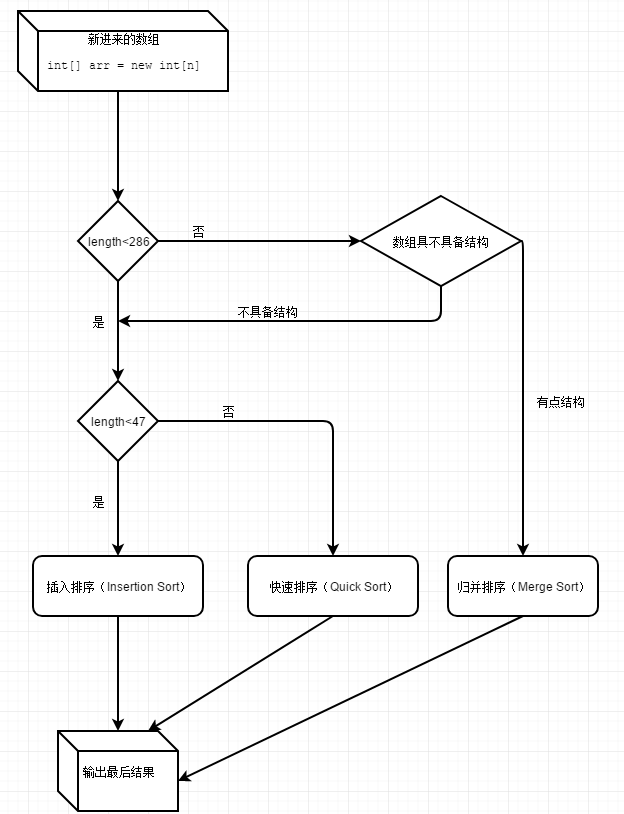
2.1 数组是否具备特定结构

在判断是否使用归并排序前，要先判断数组是否具备特定结构，这是一个什么意思呢？

// Check if the array is nearly sorted
    for (int k = left; k < right; run[count] = k) {        if (a[k] < a[k + 1]) { // ascending
            while (++k <= right && a[k - 1] <= a[k]);
        } else if (a[k] > a[k + 1]) { // descending
            while (++k <= right && a[k - 1] >= a[k]);            for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) {                int t = a[lo]; a[lo] = a[hi]; a[hi] = t;
            }
        } else { // equal
            for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) {                if (--m == 0) {
                    sort(a, left, right, true);                    return;
                }
            }
        }        /*
         * The array is not highly structured,
         * use Quicksort instead of merge sort.
         */
        if (++count == MAX_RUN_COUNT) {
            sort(a, left, right, true);            return;
        }
    }

这里主要作用是看他数组具不具备结构：实际逻辑是分组排序，每个降序序列为一个组，像1,9,8,7,6,8。9到6是降序，为一个组，然后把降序的一组排成升序：1,6,7,8,9,8。然后再从最后的8开始继续往后面找。

每遇到这样一个降序组，++count，当count大于MAX_RUN_COUNT（67），被判断为这个数组不具备结构，也就是说这数据时而升时而降，波峰波谷太多，排列太过陡峭，说明不适合采用归并排序，还是使用快速排序为宜。

如果count少于MAX_RUN_COUNT（67）的，说明这个数组还有点结构，就继续往下走下面的归并排序。

2.2 双轴快排

双轴快排（DualPivotQuickSort）是快排的一种优化版本。双轴快速排序，顾名思义，取两个中心点pivot1，pivot2，且pivot≤pivot2，可将序列分成三段：x<pivot1、pivot1≤x≤pivot2，x<pivot2，然后分别对三段进行递归。基本过程如下图：

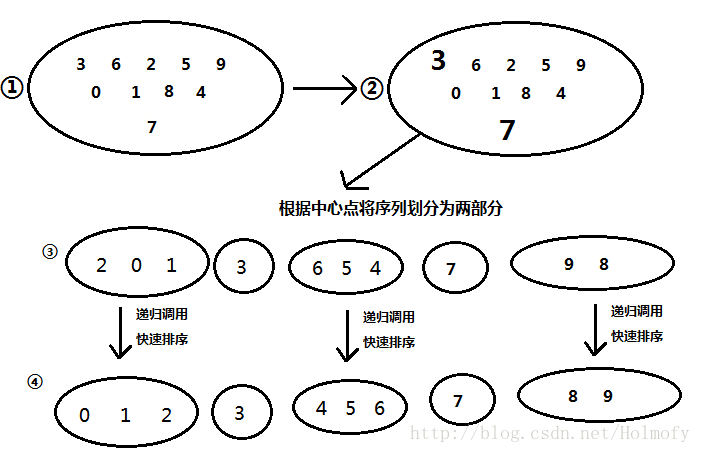
具体详细内容可见博客单轴快排（SinglePivotQuickSort）和双轴快排（DualPivotQuickSort）及其JAVA实现

3. 对象类型数组的排序

对于对象类型的数组，假设数组长度为length：

1. 如果length<32，那么采用不包含合并操作的mini-TimSort算法。
1. 如果32<=length，那么采用完整TimSort排序算法（一种结合了归并排序和插入排序的算法）。

3.1 TimSort

TimSort算法是一种起源于归并排序和插入排序的混合排序算法，设计初衷是为了在真实世界中的各种数据中可以有较好的性能。

基本工作过程是：

扫描数组，确定其中的单调上升段和严格单调下降段，将严格下降段反转。我们将这样的段称之为run。
定义最小run长度，短于此的run通过插入排序合并为长度高于最小run长度；
反复归并一些相邻run，过程中需要避免归并长度相差很大的run，直至整个排序完成；
如何避免归并长度相差很大run呢，依次将run压入栈中，若栈顶run X，run Y，run Z 的长度违反了X>Y+Z 或 Y>Z 则Y run与较小长度的run合并，并再次放入栈中。依据这个法则，能够尽量使得大小相同的run合并，以提高性能。注意Timsort是稳定排序故只有相邻的run才能归并。
Merge操作还可以辅之以galloping，具体细节可以自行研究。

总之，timsort是工业级算法，其混用插入排序与归并排序，二分搜索等算法，亮点是充分利用待排序数据可能部分有序的事实，并且依据待排序数据内容动态改变排序策略——选择性进行归并以及galloping。

具体内容我们不展开，可详见Collections.sort()源码分析(基于JAVA8)

4. 为什么要采用不同的算法？

对于长度较小的数组使用插入排序这很好理解，虽然插入排序的时间复杂度为O(n^2)，但在n较小的情况下，插入排序性能要高于快速排序。

其次我们要知道，在n的数量较大时，归并排序和快速排序，都是性能最优的排序算法，他们的时间复杂度平均都在O(nlogn)左右，只不过区别在于归并排序是稳定的，快速排序是不稳定的。

稳定是指相等的数据在排序之后仍然按照排序之前的前后顺序排列。

对于基本数据类型，稳定性没有意义，所以它可以使用不稳定的快排（当然它也使用了归并排序）

而对于对象类型，稳定性是比较重要的，因为对象相等的判断比较复杂，我们无法寄希望于每个程序员都会重写准确的equal方法，故而稳妥起见，最好相等对象尽量保持排序前的顺序，故而我们使用都是稳定算法的归并排序和插入排序结合而成的TimSort算法。

另外一个原因是归并排序的比较次数比快排少，移动（对象引用的移动）次数比快排多，而对于对象来说，比较是相对耗时的操作，所以它不适合使用快排。

而对于基本数据类型来说，比较和移动都不怎么耗时，所以它用归并或者快排都可以

总结：

基本数据类型数组使用快排+归并是因为：
- 基本数据类型无所谓稳定性，可以采用非稳定的快排。
- 对于基本数据类型来说，比较和移动都不怎么耗时，所以它用归并或者快排都可以。
对象数据类型数组使用TimSort排序是因为（或者换句话说，对象数据类型不使用快排是因为）：
- 对象数据类型要求稳定性，需要采用稳定的归并+插入。
- 对于对象来说，比较操作相对耗时，所以用比较操作较少的归并排序可以扬长避短。