1 堆和树的区别

堆是一类特殊的树，就类似一堆东西一样（金字塔结构），按照由大到小（或由小到大）“堆”起来。

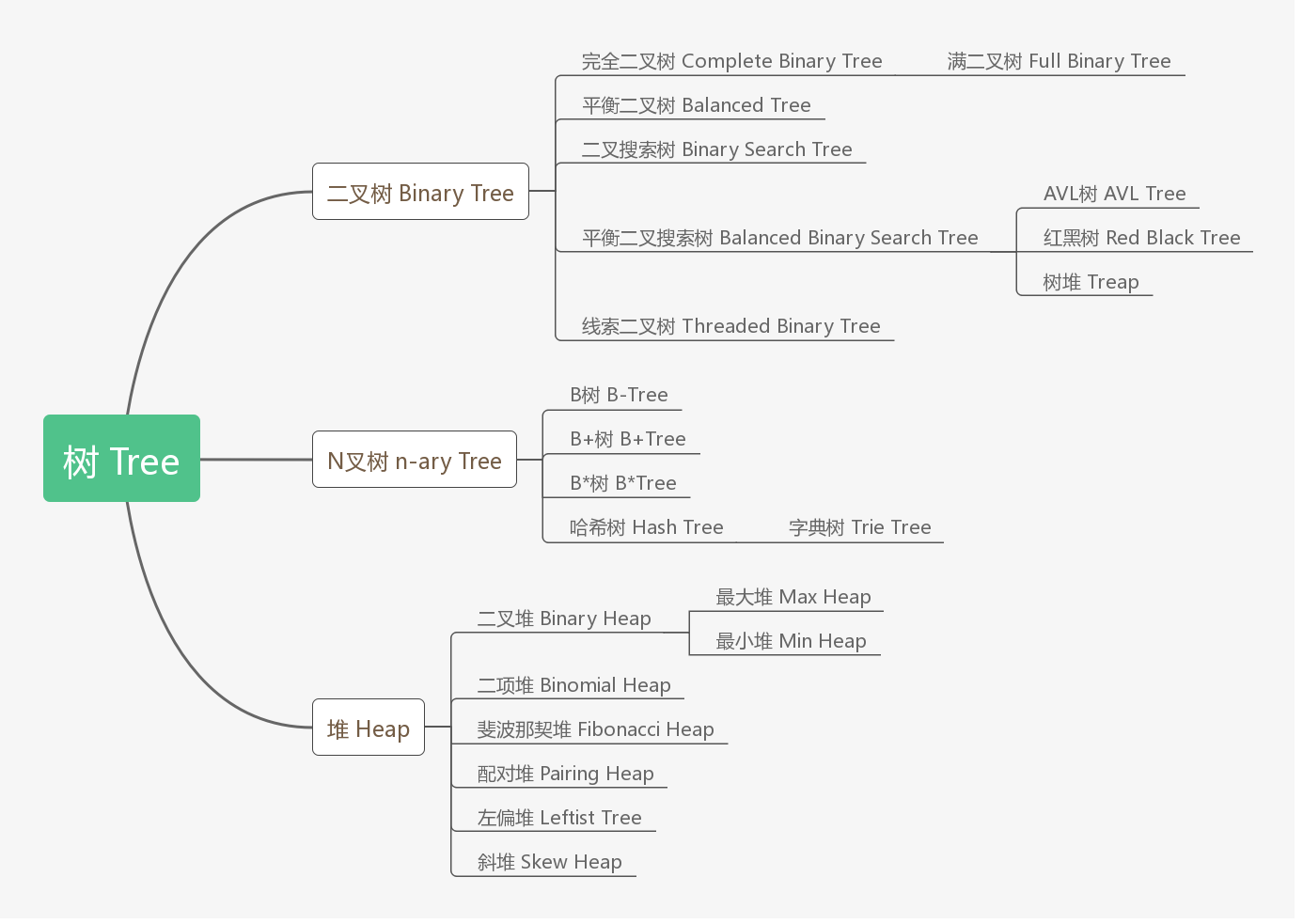
其中容易混淆的是二叉堆和二叉树。

二叉堆的特点是双亲结点的值必然小于等于（最小堆）或者大于等于（最大堆）子结点的值，而两个子结点的关键字没有次序规定。

而二叉树中，每个双亲结点的值均大于左子树结点的值，均小于右子树结点的值，也就是说，每个双亲结点的左右子结点的值有次序关系。

从上面各自的结构上的分析可得：二叉树是用来做查找的，而二叉堆是用来做排序的。

2 优先级队列

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。而在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。

优先队列具有最高级先出（first in, largest out）的行为特征。通常采用堆数据结构来实现，因为和其他线性结构相比，用堆实现优先级队列的性能最优：

一般在优先队列里面说“堆”这个词，指的都是二叉堆这种数据结构实现。

数据结构	入队性能	出队性能（取最大/最小元素）
普通线性结构	O(1)	O(n)
有序线性结构	O(n)	O(1)
堆	O(logn)	O(logn)

可以看到，使用堆来实现优先级队列，它的入队和出队操作性能都比较优秀且平衡。

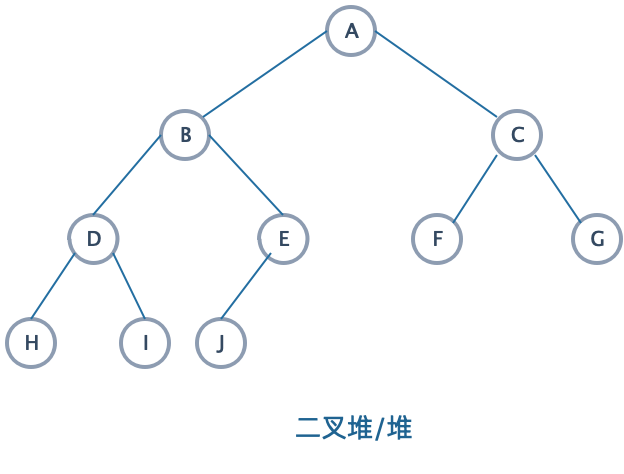
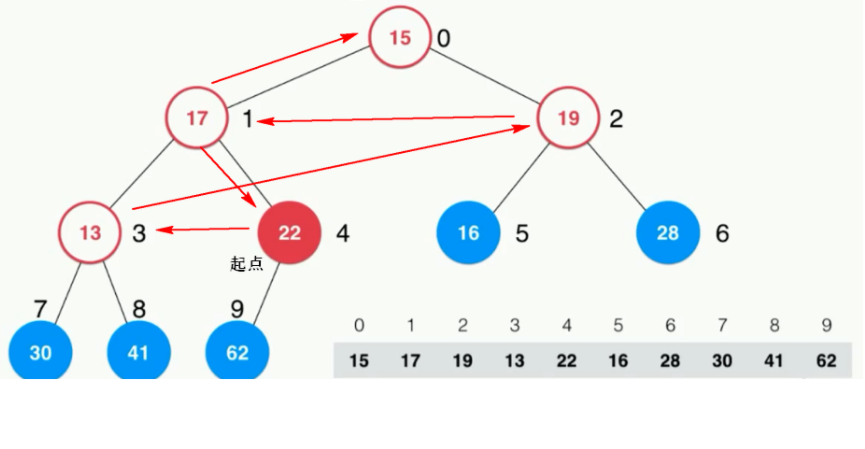
由于二叉堆具有很明显的规律，所以我们可以用一个数组而不需要用链表来表示。我们设计一个数组来表示上图的“二叉堆”。

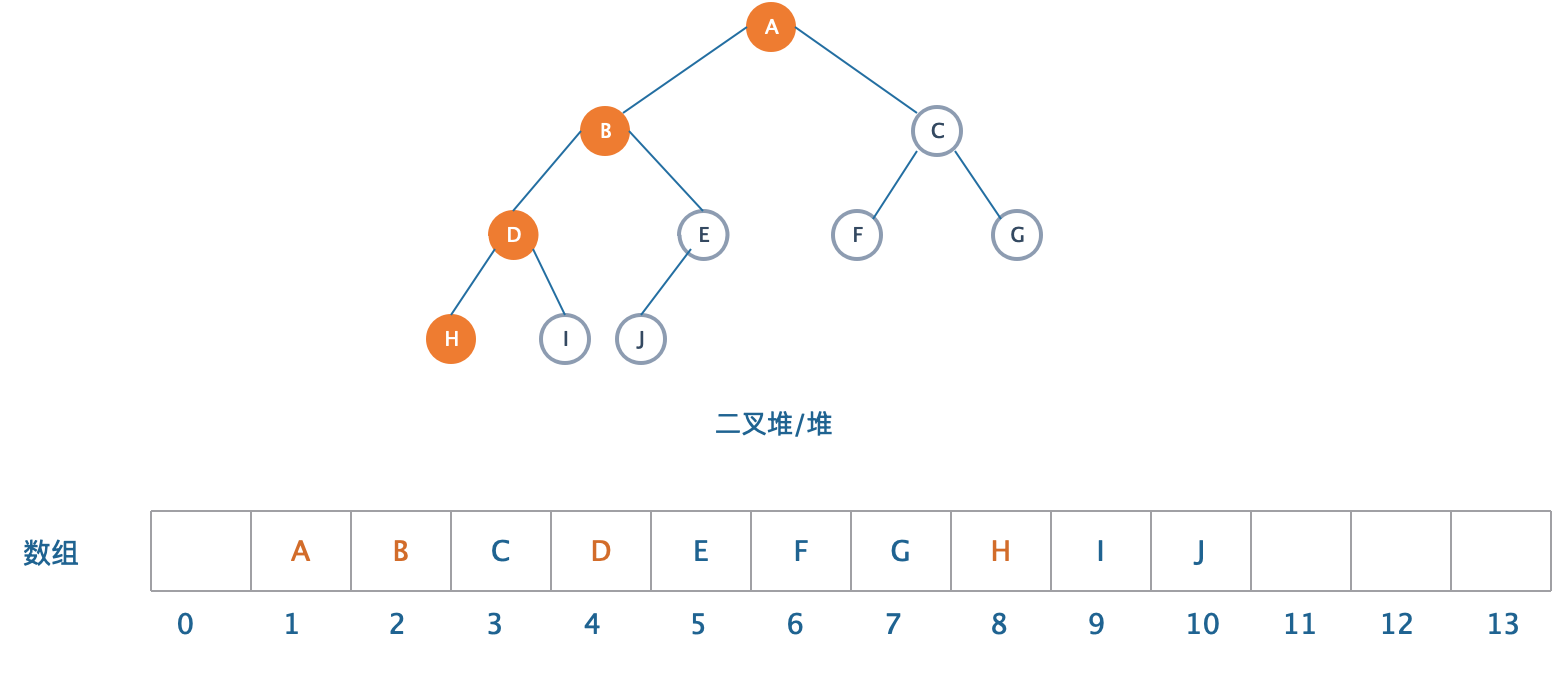
根据二叉堆的性质，我们可以得到这样的数组来表示一个堆：数组第0位放弃，从第一位开始放入堆的元素。我们看到，在堆中描述的父子结构（颜色标记），在数组中依然得以保留，不过保留的方式变成了：第i个位置上的元素，他的左子结点总是在第2i位置上，右子结点在2i+1的位置上。

2.1 入队操作(add)

就像为了保证二叉树的查询效率，我们要时刻维持二叉树的平衡一样。我们每次对堆进行插入操作，都需要保证满足堆的堆序特性。所以很多时候我们在插入之后，不得不调整整个堆的顺序来维持堆的数据结构。

这个在插入时能保证堆继续“平衡”的操作叫做上滤（Sift up），下面以一个最小堆为例：

为将一个元素X插入到堆中，我们在下一个可用位置（前序遍历找下一个可用结点）创建一个空穴。
如果X可以放在该空穴中而不破坏堆的序（父结点小于等于子结点），那么可以插入完成。否则，将空穴和父结点交换位置。这个操作叫做上滤。

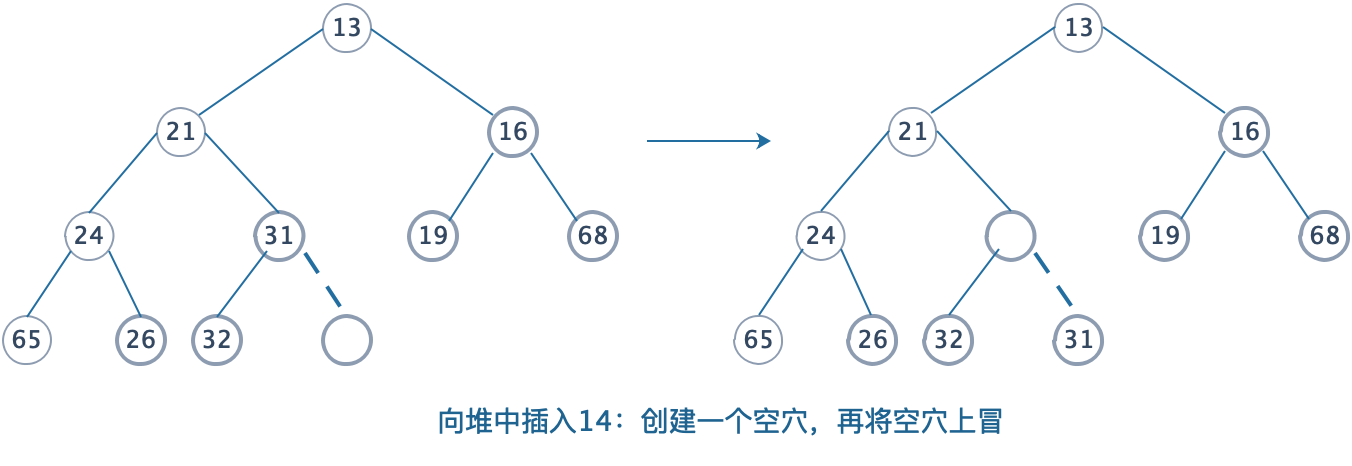
以此类推，直到空穴无法再上滤为止（此时的父结点已经小于等于插入的值），插入完成。

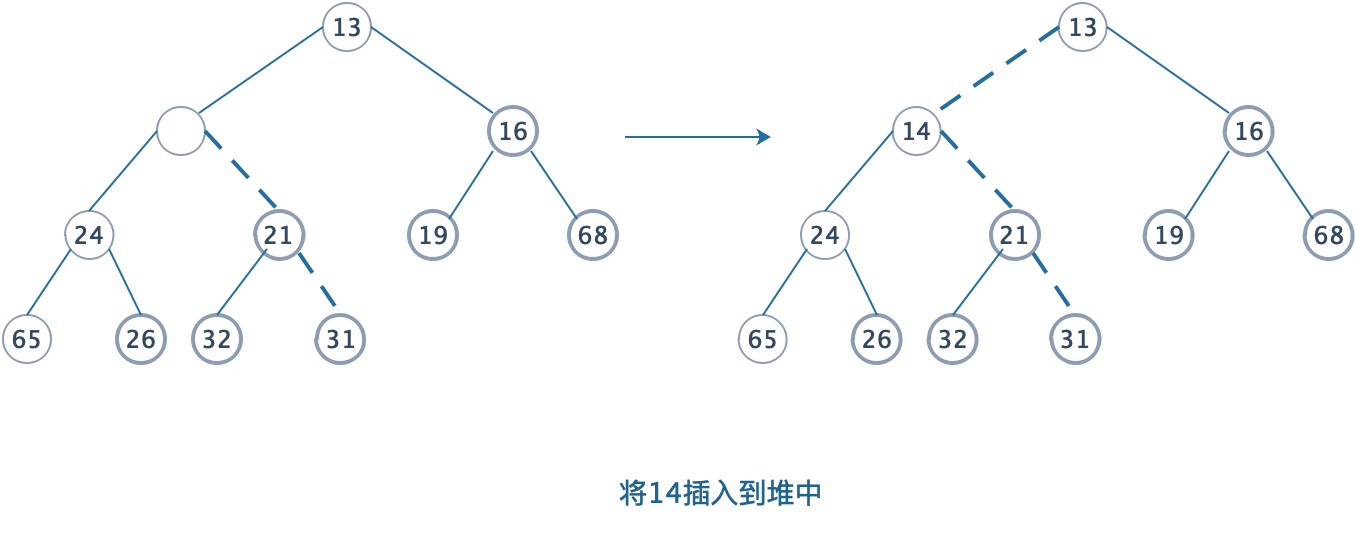
这个操作我们可以通过递归来实现，平均的时间复杂度是O(logn)。

2.2 出队操作(poll)

根据堆序特性，找到最先元素很简单，就是堆的根节点，但是删除它却不容易，删除根节点，必然会破坏树的结构。所以在删除时，我们也要特定操作，来保证堆序继续正确。

这个在删除时能保证堆继续“平衡”的操作叫做下滤（Sift down），下面还是以一个最小堆为例：

删除一个元素，我们可以很快找到，根节点元素就是最小的元素。此时根节点变成了空穴。删掉了一个结点，肯定要找一个结点补回来，为了维持完全二叉的特性，我们找堆的最后一个结点（前序遍历）赋值给空穴。也就是下图中标红的31。
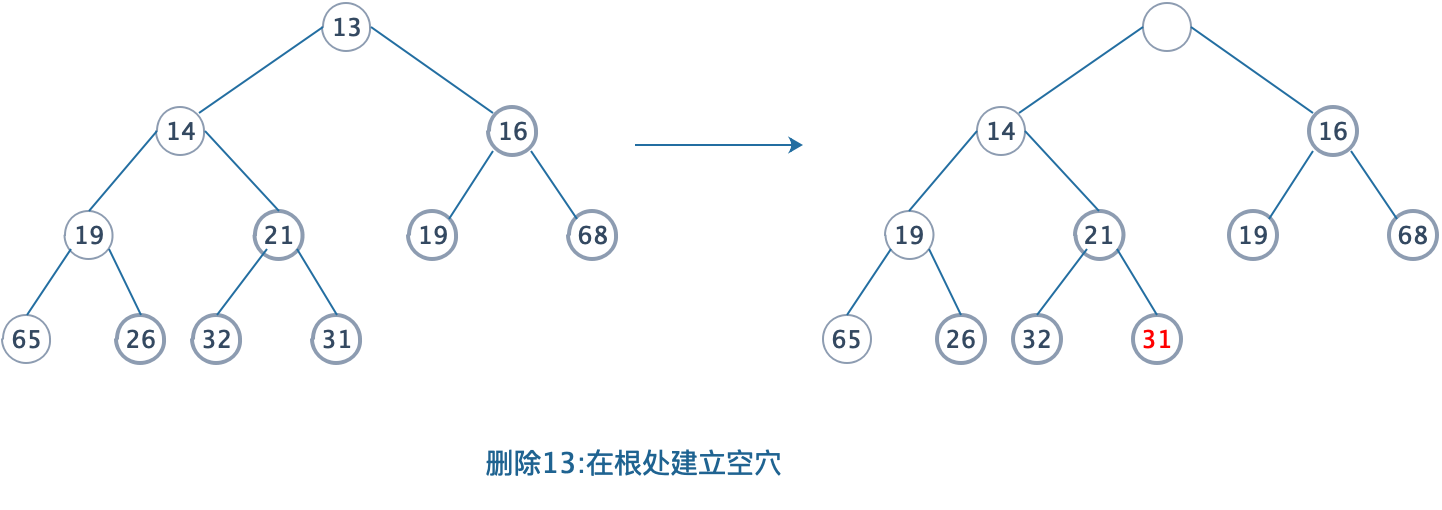
此时，31成为了根结点是不满足堆序的，所以肯定需要在左右结点中找一个子结点来和根结点做交互，选择哪个呢？根据堆序，肯定选择子结点中较小的那个结点，和空穴交换位置。
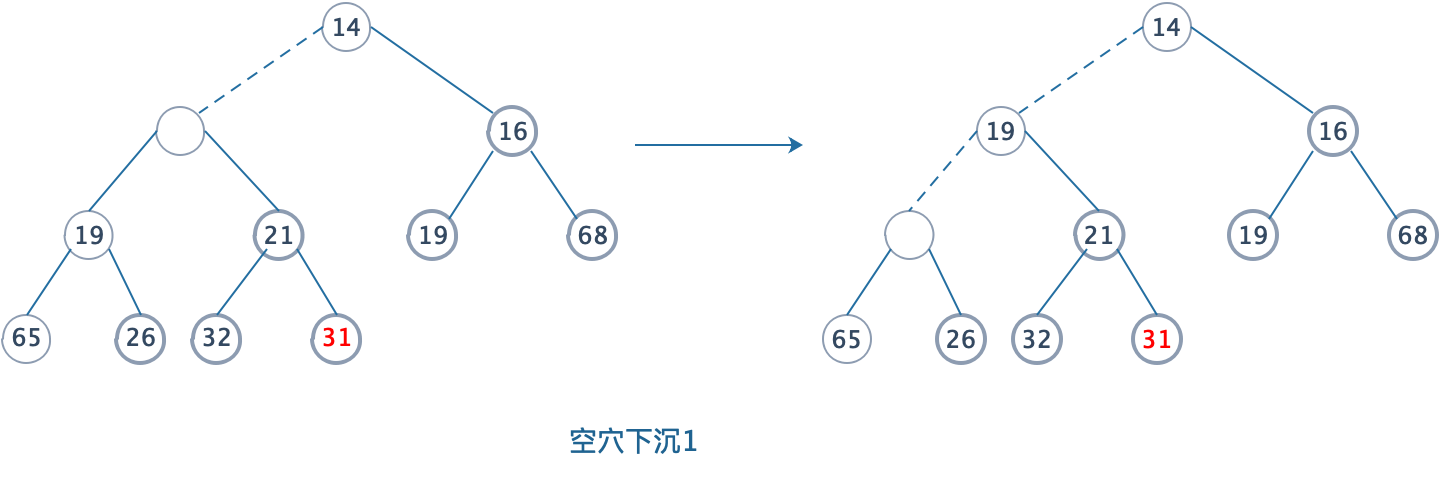
重复上述操作，直到空穴下沉到最底层为止。下滤操作完成。

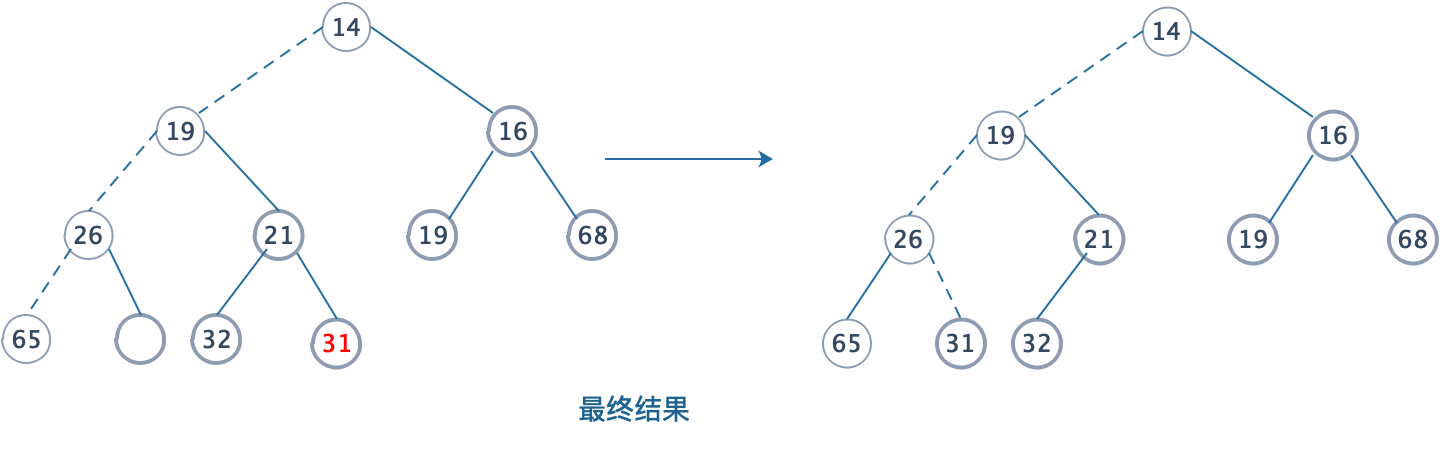
这个操作我们可以通过递归来实现，平均的时间复杂度是O(logn)。

2.3 构建堆(heapify)

将一个任意数组整理成堆，这个操作叫做heapify，构建一个n个元素的最大/最小堆，我们直接执行n次insert方法即可，因为在设计insert方法时，就已将考虑到将插入到值放到堆的合适位置。输入n项，即可自动生成n大小的堆。此时算法的时间复杂度是O(nlogn)。

2.4 替换堆中堆顶元素(replace)

用一个新的元素，替换堆中优先级最高的元素，可以直接用新元素覆盖堆顶元素，然后执行一次sift down操作即可，时间复杂度为O(logn)。

3 JAVA中PriorityQueue实现

PriorityQueue在jdk的java.util包下，其本质是一个Object数组，也就是我们前文提到的，使用数组来存放堆的模式：

/**
 * Priority queue represented as a balanced binary heap: the two
 * children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
 * priority queue is ordered by comparator, or by the elements'
 * natural ordering, if comparator is null: For each node n in the
 * heap and each descendant d of n, n <= d.  The element with the
 * lowest value is in queue[0], assuming the queue is nonempty.
 */
transient Object[] queue; // non-private to simplify nested class access

3.1 构造方法

优先级队列，java的实现默认是小顶堆的实现，默认调用Object的compareTo方法。

1	PriorityQueue queue = new PriorityQueue();

我们可以使用它的另一个构造方法，手动传入指定的comparator：

Comparator comparator = new Comparator() {
	@Override
	public int compare(Object o1, Object o2) {
		...
	}
};
PriorityQueue queue = new PriorityQueue(capacity,comparator);

3.2 添加元素

add()和offer()都是用来做入队操作的方法，add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同。

add()在插入失败时抛出异常，offer()则会返回false。对于PriorityQueue，这两个方法其实没什么差别。新加入的元素可能会破坏堆的堆序性质，因此需要进行必要的调整。

public boolean offer(E var1) {
	if (var1 == null) {//不允许放入null元素
		throw new NullPointerException();
	} else {
		++this.modCount;
		int var2 = this.size;
		if (var2 >= this.queue.length) {
			this.grow(var2 + 1);//自动扩容
		}

		this.size = var2 + 1;
		if (var2 == 0) {//队列原来为空，这是插入的第一个元素
			this.queue[0] = var1;
		} else {
			this.siftUp(var2, var1);//调整
		}

		return true;
	}
}

上述代码中，扩容函数grow()类似于ArrayList里的grow()函数，就是再申请一个更大的数组，并将原数组的元素复制过去，这里不再赘述。需要注意的是siftUp(int k, E x)方法，该方法用于插入元素x并维持堆的特性。

private void siftUp(int var1, E var2) {
	if (this.comparator != null) {
		this.siftUpUsingComparator(var1, var2);// 元素类型是无法直接比较，要借用比较器的场景
	} else {
		this.siftUpComparable(var1, var2);// 元素类型是可以直接比较，不需要借用比较器的场景
	}

}

这两者代码大同小异，我们看其中一个：

private void siftUpUsingComparator(int var1, E var2) {// var1是size
	while(true) {
		if (var1 > 0) {
			int var3 = var1 - 1 >>> 1;// val3是parent的下标，parentNo = (nodeNo-1)/2
			Object var4 = this.queue[var3]; // val4是parent元素
			if (this.comparator.compare(var2, var4) < 0) {
				this.queue[var1] = var4;// 如果var2优先级较高，和parent交换下标
				var1 = var3;
				continue;
			}
		}
		this.queue[var1] = var2;// 交换完下标，最后赋值，var2赋值到它应该去的地方。
		return;
	}
}

3.3 获取队首元素

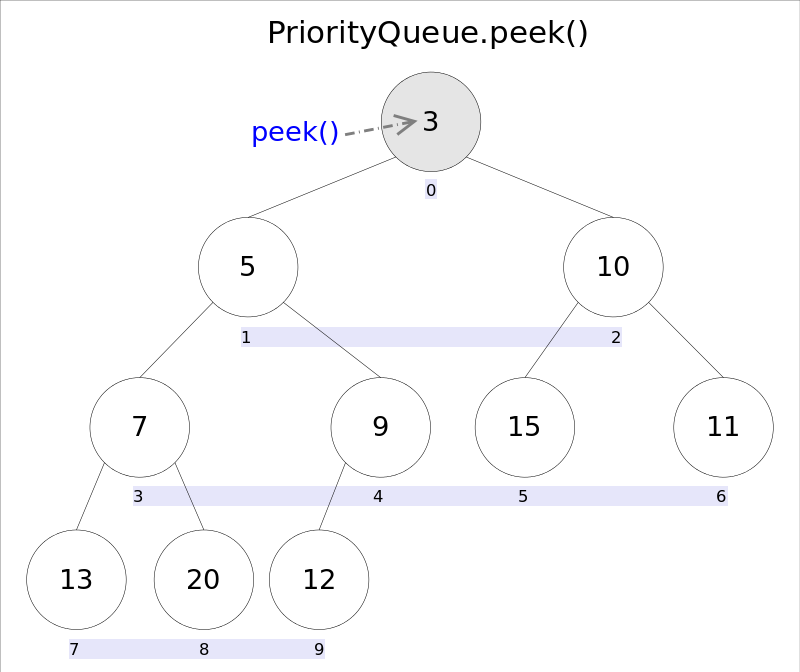
element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值优先级最高的那个元素。

二者唯一的区别是当方法失败时element()抛出异常，peek()返回null。

由于堆用数组表示，根据下标关系，0下标处的那个元素就是堆顶元素。所以直接返回数组0下标处的那个元素即可。

1
2
3

public E peek() {
	return (size == 0) ? null : (E) queue[0];
}

3.4 删除队首元素

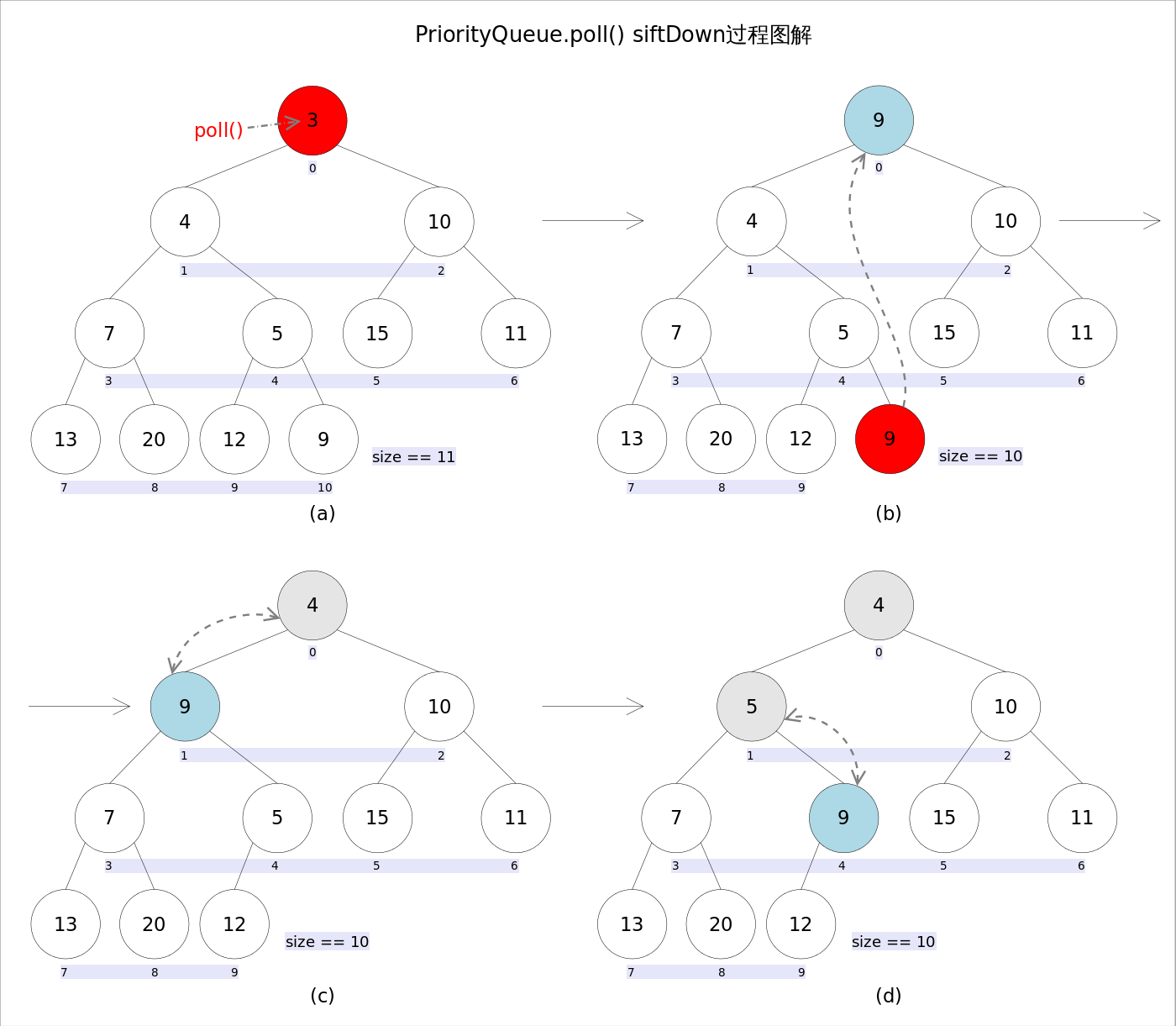
remove()和poll()的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时remove()抛出异常，poll()返回null。由于删除操作会改变队列的结构，为维护堆的堆序性质，需要进行必要的调整。

public E poll() {
	if (size == 0)
		return null;
	int s = --size;//size减小
	modCount++;
	E result = (E) queue[0];//0下标处的那个元素就是堆顶元素
	E x = (E) queue[s];
	queue[s] = null;
	if (s != 0)
		siftDown(0, x);//调整
	return result;
}

上述代码首先记录0下标处的元素，并用最后一个元素替换0下标位置的元素，之后调用siftDown()方法对堆进行调整，最后返回原来0下标处的那个元素（也就是最小的那个元素）

重点是siftDown(int k, E x)方法，该方法的作用是从k指定的位置开始，将x逐层向下与当前点的左右孩子中较小的那个交换，直到x小于或等于左右孩子中的任何一个为止。

private void siftDown(int k, E x) {
	if (comparator != null)
		siftDownUsingComparator(k, x);// 元素类型是无法直接比较，要借用比较器的场景
	else
		siftDownComparable(k, x);// 元素类型是可以直接比较，不需要借用比较器的场景
}

这两者代码大同小异，我们看其中一个：

private void siftDownUsingComparator(int k, E x) {
	int half = size >>> 1;
	while (k < half) {
		// 首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
		int child = (k << 1) + 1;//leftNo = parentNo*2+1
		Object c = queue[child];
		int right = child + 1;
		if (right < size &&
			comparator.compare((E) c, (E) queue[right]) > 0)
			c = queue[child = right];
		if (comparator.compare(x, (E) c) <= 0)
			break;// 如果parent已经比子结点小了，跳出循环
		queue[k] = c;// 否则，用较小的子结点替换parent，继续循环
		k = child;
	}
	queue[k] = x;最后将x赋值在他适合的位置
}

3.5 删除特定元素

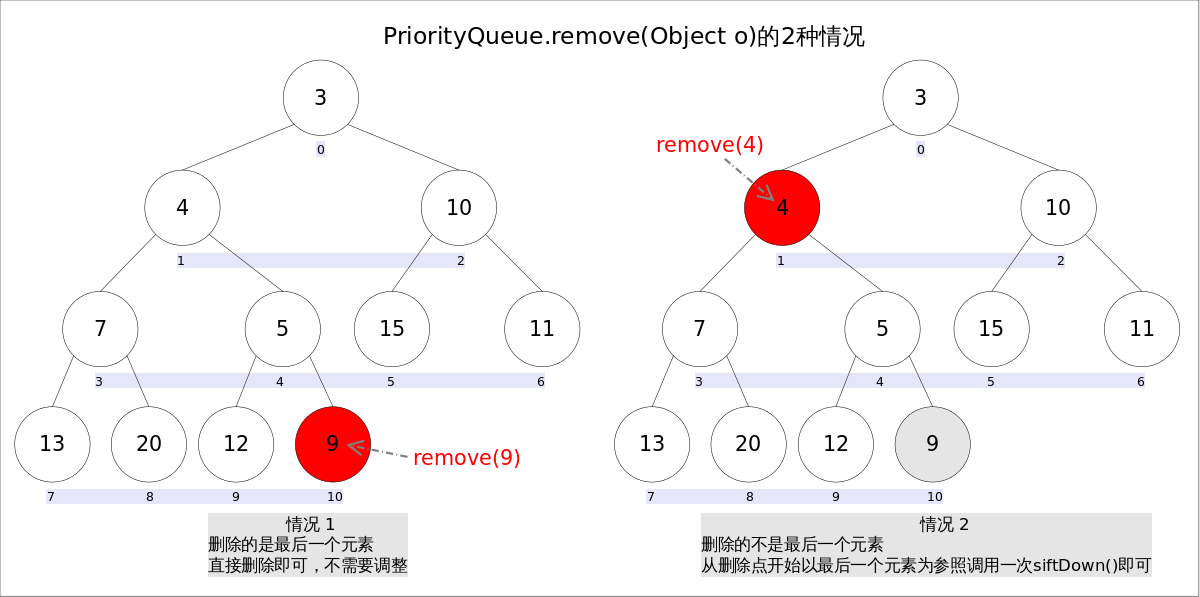
remove(Object o)方法用于删除队列中跟o相等的某一个元素（如果有多个相等，只删除一个），该方法不是Queue接口内的方法，而是Collection接口的方法。由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。

具体来说，remove(Object o)可以分为2种情况：

删除的是最后一个元素。直接删除即可，不需要调整。
1. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次siftDown()即可。此处不再赘述。

public boolean remove(Object o) {
	int i = indexOf(o); //通过遍历数组的方式找到第一个满足o.equals(queue[i])元素的下标
	if (i == -1)
		return false;// 找不到下标，就返回
	else {
		removeAt(i);// 调用removeAt
		return true;
	}
}

private E removeAt(int i) {
	// assert i >= 0 && i < size;
	modCount++;
	int s = --size;
	if (s == i) // removed last element
		queue[i] = null;// //情况1，也就是要删的地方是堆的最后一个，则直接删除
	else {
		E moved = (E) queue[s];// 将堆最后一个元素赋给moved
		queue[s] = null;
		siftDown(i, moved);// 情况2，则用moved来替换被删除的位置，接着执行siftDown方法，
		if (queue[i] == moved) {// 如果调用完siftDown，但moved还在原位没有下沉，那么可能说明moved应该上滤
			siftUp(i, moved);// 调用siftUp，尝试让moved上滤
			if (queue[i] != moved)// moved终于不在原地了
				return moved;
		}
	}
	return null;
}

4 应用

4.1 在n个元素中找到前k项

维护一个size=k的优先级队列，优先级的逻辑为题目中要求的逻辑，如题目要是找出最小的k项，那实现就是值越大的项优先级越高。

遍历一次n个元素，每次遍历中，都将当前元素入队，同时出队一个元素，保证队列的长度为k。

这样一次完整的遍历后，队列中的元素即为结果，时间复杂度为n*(logk+logk)，即O(nlogk)。

不过该题使用不完整快排（即快排到前k项即可，其他的操作都不用做）会更快，可以达到O(n)。