前言
二叉树的遍历是指不重复地访问二叉树中所有结点,主要指非空二叉树,对于空二叉树则结束返回。二叉树的遍历主要包括前序遍历、中序遍历、后序遍历。
一棵二叉树由根结点、左子树和右子树三部分组成,若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树,则二叉树的遍历方式有 6 种:DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别,所以默认都是先左后右,故而只讨论三种方式:
- DLR–前序遍历(根在前,从左往右,首先访问根结点,然后遍历左子树,最后遍历右子树,根->左->右)
- LDR–中序遍历(根在中,从左往右,首先遍历左子树,然后访问根节点,最后遍历右子树,左->根->右)
- LRD–后序遍历(根在后,从左往右,首先遍历左子树,然后遍历右子树,最后访问根节点,左->右->根)
- 层序遍历(除此之外,还有一种层序遍历,层序遍历嘛,就是按层,从上到下,从左到右遍历,这个没啥好说的)
所以前中后序遍历的前/中/后,指的是根节点在前/中/后输出的意思,因此这三种遍历也称为先根遍历,中根遍历,后根遍历。
本文就不掉书袋再复述前序/中序/后序遍历的教科书方法了。我们这里介绍一种易记的方法。
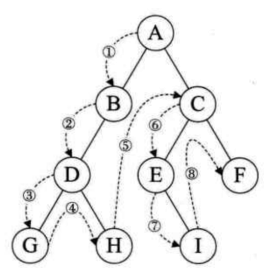
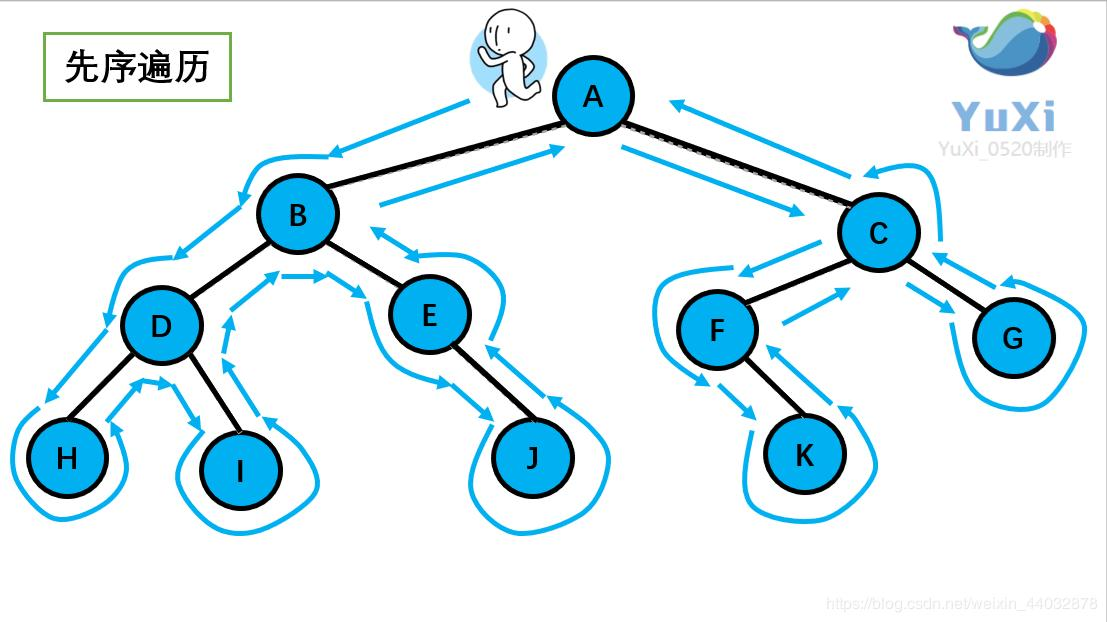
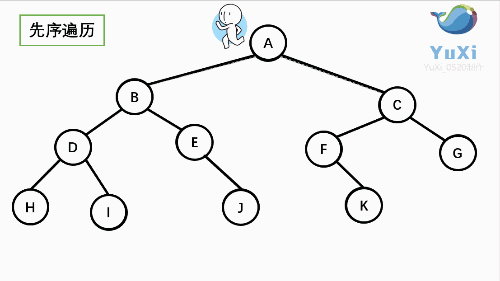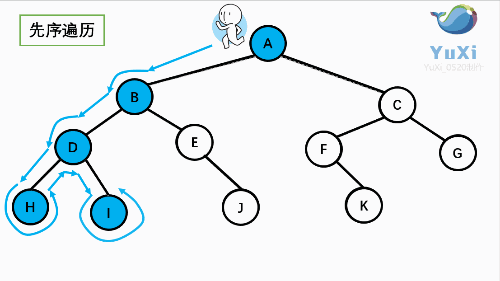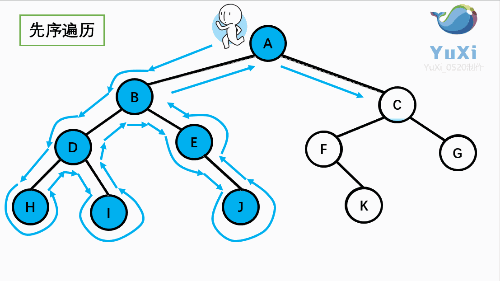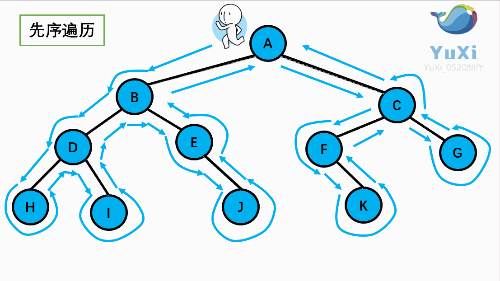
1 先序遍历
先序遍历可以想象成,小人从树根开始绕着整棵树的外围转一圈,经过结点的顺序就是先序遍历的顺序
先序遍历结果:ABDHIEJCFKG
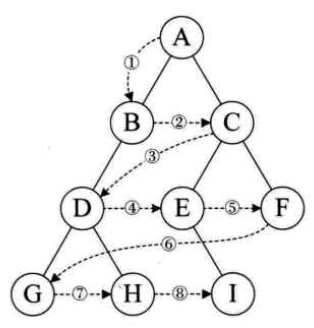
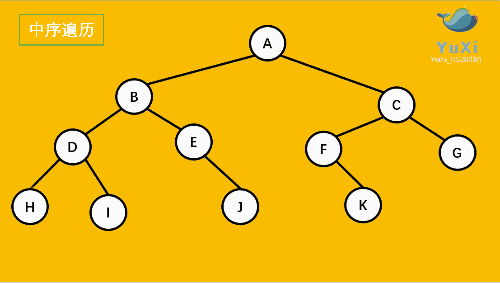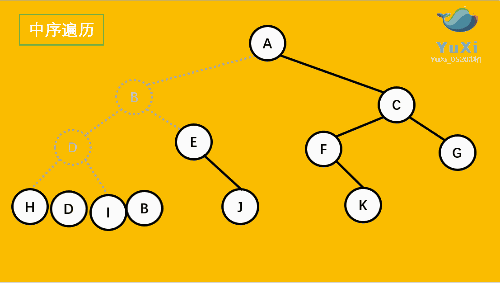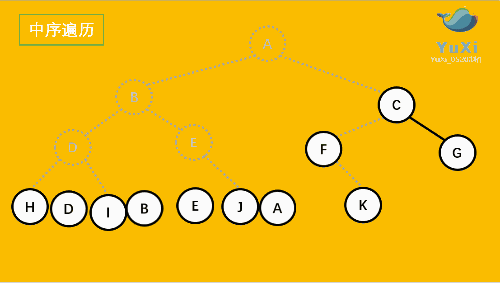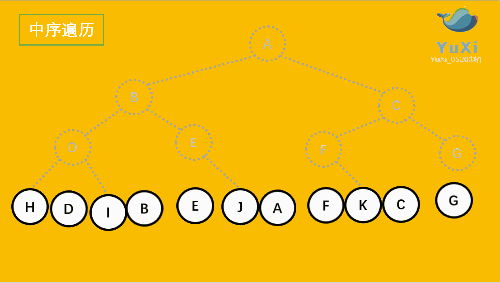
2 中序遍历
中序遍历可以想象成,按树画好的左右位置投影下来就可以了
中序遍历结果:HDIBEJAFKCG
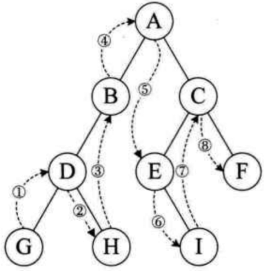
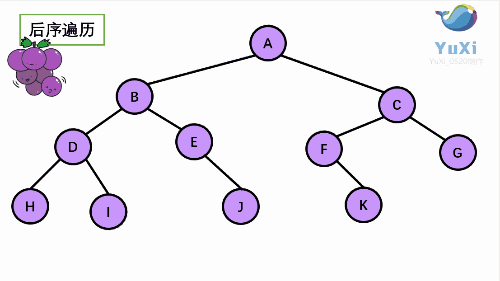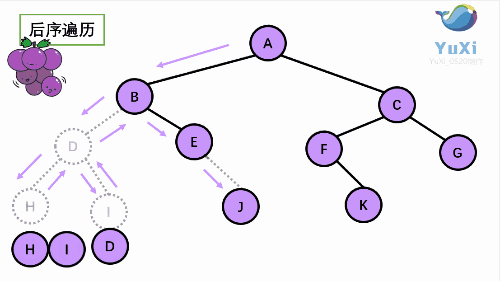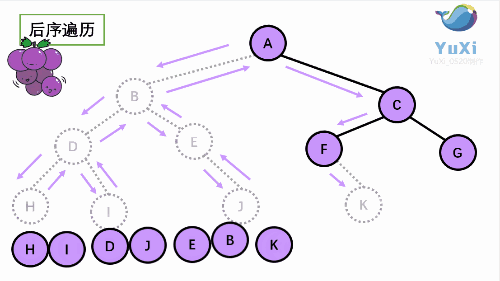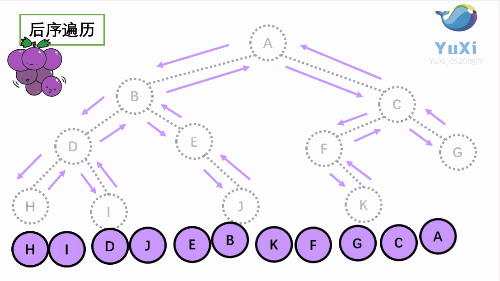
3 后序遍历
后序遍历就像是剪葡萄,我们要把一串葡萄剪成一颗一颗的。还记得我们先序遍历绕圈的路线么?就是围着树的外围绕一圈,如果发现一剪刀就能剪下的一颗葡萄(注意必须是一颗葡萄),就把它剪下来,组成的就是后序遍历了。
后序遍历结果:HIDJEBKFGCA
4 层序遍历
层序遍历太简单了,就是按照一层一层的顺序,从左到右写下来就行了。
后序遍历结果:ABCDEFGHIJK