1 动态规划的概念

1.1 定义

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的数学方法。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。

决策过程是什么呢？在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。各个阶段决策的选取依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线。这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。

在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前的状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法。

1.2 概念和术语

关于动态规划，我们要了解如下概念和术语，我们以0-1背包问题为例：

0-1背包问题:我们有n种物品，物品j的重量为wj，价格为pj，背包的总重量是W，如果限定每种物品只能选择0个或1个，那么如何选取物品，使背包内物品的总价值最大。

阶段：
- 把所给求解问题的过程恰当地分成若干个相互联系的阶段，以便于求解，过程不同，阶段数就可能不同
- 0-1背包问题中，我们每一次选取一个新的物品放入背包的这个过程，就是一个阶段。
状态：
- 状态表示每个阶段开始面临的自然状况或客观条件，它不以人们的主观意志为转移，也称为不可控因素。
- 0-1背包问题中，我们每一次选取一个新的物品后，（已选取物品，已选取的物品总价值），这二者的值就是一个阶段的状态。
决策
- 一个阶段的状态给定以后，从该状态演变到下一阶段某个状态的一种选择（行动）称为决策。
- 0-1背包问题中，每次我们选取哪个物品放入，这就是一个决策，
策略：
- 由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程，可供选取的策略有一定的范围限制，这个范围称为允许策略集合。策略不同，效果也不同，多阶段决策问题，就是要在可以选择的那些策略中间，选取一个最优策略，使在预定的标准下达到最好的效果。
- 一次连续阶段的多个决策序列就是策略，比如策略A可以是：放入钢笔——放入水壶——放入睡袋。策略B是放入钢笔——放入睡袋——放入头盔。以此类推
多阶段决策问题：
- 如果一类活动过程可以分为若干个互相联系的阶段，在每一个阶段都需作出决策（采取措施），一个阶段的决策确定以后，常常影响到下一个阶段的决策，从而就完全确定了一个过程的活动路线，则称它为多阶段决策问题
- 0-1背包问题就是一个典型的多阶段决策问题。

1.3 核心思路

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

不过与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。

如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。在动态规划中，我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

动态规划的核心除了分阶段决策外，还有上面所说的避免重复计算。这个如何理解呢？

比如0-1背包问题，我们现在有1，2，3三个物品，xj=1表示j物品放入背包，xj=0则表示j物品没放入。同时策略C(x1x2x3)=001，表示x1和x2都没有放入背包，x3放入了背包。

现在假如通过穷举得到了如下的5种可行策略：

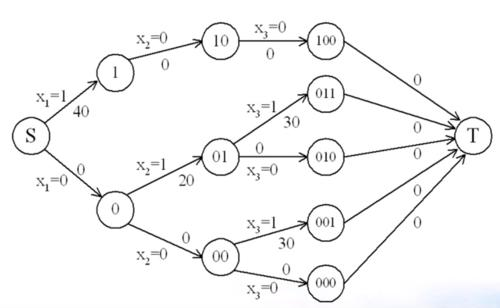
那么由图我们可以知道，C2=011和C3=010这两种策略，都要经过01这个策略，如果在计算011的时候我们计算一遍01，在计算010的时候我们又计算一遍01，那么就重复计算了，我们为什么不把01这个策略的状态（已选取物品，已选取的物品总价值）保存下来呢？这样在计算010的时候，直接就可以把01的结果拿出来用了。

动态规划算法可以理解为是分治法和穷举法的结合：

它用分治法的思想将一个问题分为多个决策阶段，既将问题复杂性减小，也为后续的局部结果复用提供前提。
它搜索解的方式还是穷举法那一套，只不过因为可以局部复用，所以它的复杂性会大大降低。

其关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受，而搜索算法在时间上却无法承受，所以我们舍空间而取时间

1.4 适用场景

动态规划算法通常用于求解具有某种最优性质的多阶段决策问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。

任何思想方法都有一定的局限性，超出了特定条件，它就失去了作用。同样，动态规划也并不是万能的。适用动态规划的问题必须满足最优化原理和状态无后效性：

最优化原理（最优子结构性质）
- 最优化原理可这样阐述：一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。
- 在0-1背包问题中，我们假设策略C=011是最优解，也就是说背包存放x2和x3，才能使价值最高，那么它的子策略，01x和x11，也同样都是最优解。最优化原理通俗的讲就是：011是最优解，那么01x肯定也是最优解，01x表示x3先不论，x1肯定不能选，x2肯定要选，否则就不是最优解。
状态无后效性：
- 状态无后效性指的是每个阶段的状态都是过去阶段的一个完整总结，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策。这就是无后向性，又称为无后效性。
- 在0-1背包问题中，我们的状态是（已选取物品，已选取的物品总价值），我们之所以选择这样的两个值作为状态，就是因为它都是对过去阶段的完整总结。这使得从这个状态基础上进行的新的决策，可以不用去关心之前的状态，因为之前的状态被总结了。之所以要使状态无后效性，就是为了便于存储和复用阶段的结果，避免重复计算。
- 试想一下，如果状态不是无后效性的，比如我们选择的状态是（本次选取的物品），那么我们保存这个状态的值，根本对后面的复用没有帮助，后面要想知道背包还剩多少空间，还是要把之前经历过的阶段的解都计算一遍。

1.5 解题技巧

前文我们提到过，动态规划是分治法和穷举法的结合，同时，在动态规划中，我们可以用一个表来记录所有已穷举出的已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。具体的动态规划算法多种多样，但它们具有相同的填表格式。

那么，如何将上述的经验整理成解题技巧呢？还是用0-1背包问题为例，来看下所谓的填表格式到底是什么：

假设你是个小偷，背着一个可装4磅东西的背包。你可盗窃的商品有如下3件。为了让盗窃的商品价值最高，你该选择哪些商品？

商品名称	重量（磅）	价值（美元）
音响	4	3000
笔记本电脑	3	2000
吉他	1	1500

每个动态规划算法都从一个填表的网格开始，背包问题的网格如下：

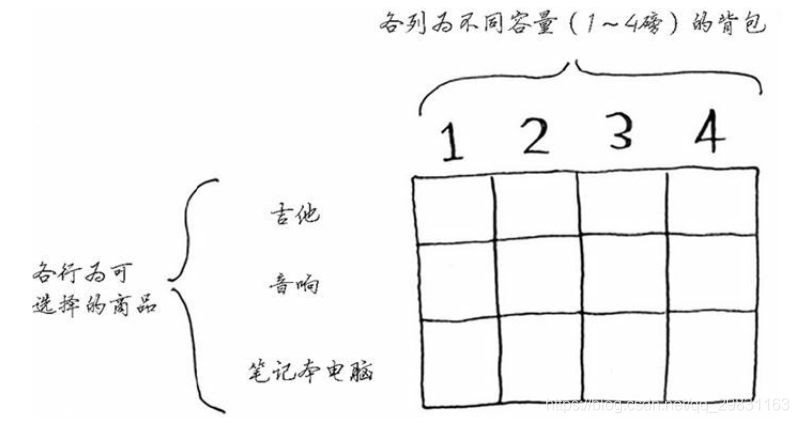
网格的各行为商品，各列为不同容量（1～4磅）的背包。单元格内填入当前情况下的最大背包价值。
第一行表示只能选吉他，第二行表示可以选吉他+音响，以此类推。
虽然我们题目的背包是4磅，但我们仍然需要1到3磅的前三列，因为它们将帮助我们在计算剩余空间时发挥作用。
网格最初是空的。我们将填充其中的每个单元格，网格填满后，就找到了问题的答案！

【填充第一行】

第一个单元格表示背包的容量为1磅。吉他的重量也是1磅，这意味着它能装入背包！因此这个单元格包含吉他，价值为1500美元。

由于这是第一行，只有吉他可供你选择，于是不管背包多大，单元格内的值都是1500美元，所以第一行的值都是1500。

【填充第二行】

我们现在处于第二行，可偷的商品有吉他和音响。我们先来看第一个单元格，它表示容量为1磅的背包。在此之前，可装入1磅背包的商品的最大价值为1500美元，由于容量1磅的背包装不下音响，因此最大价值依然是1500美元。接下来的两个单元格的情况与此相同。在这些单元格中，背包的容量分别为2磅和3磅，而以前的最大价值为1500美元。由于这些背包装不下音响，因此最大价值保持不变。

但如果背包的容量为4磅，那就能够装下音响！原来的最大价值为1500美元，但如果在背包中装入音响而不是吉他，价值将为3000美元！你更新了最大价值！在这个网格中，你逐步地更新最大价值。

于是我们得到了第二行：

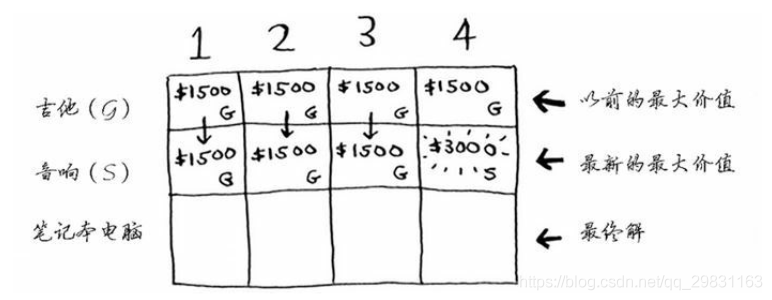
【填充第三行】

笔记本电脑重3磅，没法将其装入容量为1磅或2磅的背包，因此前两个单元格的最大价值还是1500美元。

对于容量为3磅的背包，原来的最大价值为1500美元，但现在你可选择盗窃价值2000美元的笔记本电脑而不是吉他，这样新的最大价值将为2000美元！

对于容量为4磅的背包，当前的最大价值为3000美元，你可不偷音响，而偷笔记本电脑，但它只值2000美元。价值没有原来高。但笔记本电脑的重量只有3磅，背包还有1磅的容量没用！

在1磅的容量中，可装入的商品的最大价值是多少呢？根据之前计算的最大价值可知（第一列中最大的值），在1磅的容量中可装入吉他，价值1500美元。

注意，此时我们就用到了背包容量为1的那一列，所以我们之所以要算出与4磅无关的容量为1,2,3磅的结果，就是为了这一刻。

笔记本电脑和吉他的总价值为3500美元，因此偷它们是更好的选择。最终的网格类似于下面这样。

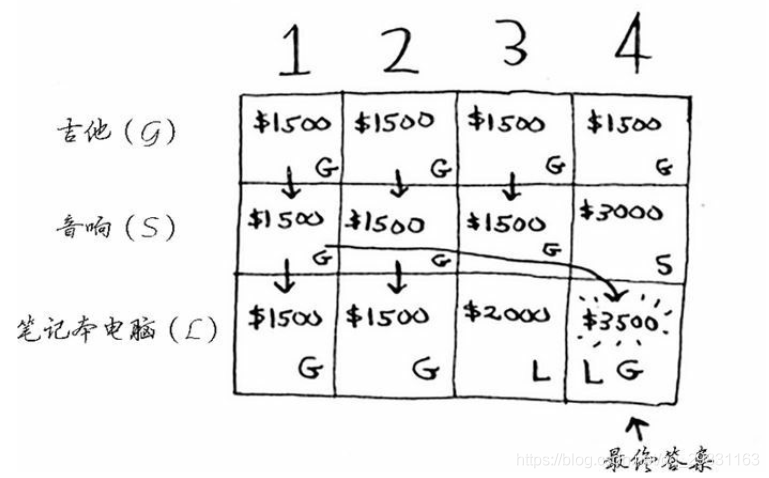
【总结】

经过上面的分析，我们可以发现，题目所要的答案，其实只是网格最右下角的那一个单元格。那我们为什么要算出其他的单元格呢？

因为下一个单元格的值，需要用到之前单元格的值来计算，比如最后的答案3500美元，就用到了背包容量为1的那一列的数据来计算剩余1磅空间的时候选择哪个物品最合算。

我们记录下之前单元格的值，就是为了计算新单元格的时候不用重复计算，就像这道题，我们最后想知道背包容量为1时应该如何选取物品，如果没有保存下结果，那我们要重新算一遍第一列的场景，那效率就很低了。

记忆化搜索，即用一个二维数组保存已经计算好的子问题的解，下次再计算相同子问题时，就不用重复求解了。

每一个新的单元格的值，都需要复用到之前单元格的数据来算出，如果我们能归纳出一个通用的以旧单元格值推导出新单元格值的公式，那就相当于找到了一条可得到最优解的方法。这个公式，我们称为状态转移方程。

我们前文提到过，状态是每一个阶段的总结，动态规划是多阶段决策的过程，我们在多个阶段间行进，状态也在一直转移。状态转移方程，顾名思义，就是状态变化的方程，比如说我们可以归纳出该题的状态转移方程如下图：

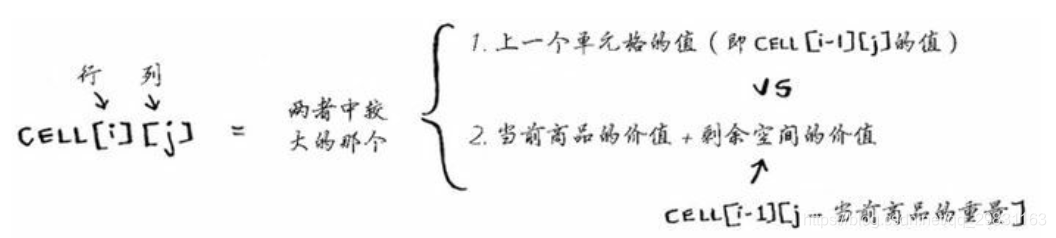
于是我们知道了：

填表法是动态规划的固定套路，它能帮助我们理解状态转移的过程，并且记录和复用之前的结果。
网格的每一个单元格，都可以理解为是一个阶段，阶段变量有两个，可选取物品类型和背包重量，也就是网格的横纵轴。
每个阶段的策略，就是我们的状态转移方程，即我们用现有的状态，决策出了当前阶段的状态。
动态规划的核心就在于：
- 将题目划分为多个子问题，对应多个阶段
- 确定哪些变量属于状态
- 归纳出状态转移方程

2 经典题型

2.1 0-1背包问题

2.1.1 题目

【描述】：有 n 个物品和一个大小为 bagSize 的背包. 给定数组 itemSizes 表示每个物品的大小和数组 itemValues 表示每个物品的价值。问最多能装入背包的总价值是多大?

itemSizes[i], itemValues[i], n, bagSize 均为整数
你不能将物品进行切分
你所挑选的要装入背包的物品的总大小不能超过 bagSize
每个物品只能取一次

【样例 1】:

输入: bagSize = 10, itemSizes = [2, 3, 5, 7], itemValues = [1, 5, 2, 4]
输出: 9
解释: 装入 itemSizes[1] 和 itemSizes[3] 可以得到最大价值, itemValues[1] + itemValues[3] = 9

【样例 2】:

输入: bagSize = 10, itemSizes = [2, 3, 8], itemValues = [2, 5, 8]
输出: 10
解释: 装入 itemSizes[0] 和 itemSizes[2] 可以得到最大价值, itemValues[0] + itemValues[2] = 10

2.1.2 题解

前文已叙述，不再赘述。

2.1.3 代码

public int backPack(int bagSize, int[] itemSizes, int[] itemValues) {
    int itemsNum = itemSizes.length;
    // 创建一个数组，存放已计算过的结果，填表法。
    int[][] values = new int[itemsNum][bagSize];
    // 开始填表，itemSizes数组中，0-itemIdx区间内的物品，为当前可选物品
    for (int itemIdx = 0;itemIdx < itemsNum;itemIdx++){
        for (int bagIdx = 0;bagIdx < bagSize;bagIdx++){
            int thisBagSize = bagIdx+1;// 因为下标为0开始，但背包size从1开始。
            // 从已计算的结果中获取【当前背包size下，如果当前物品不可取时，背包可存放的最大价值】。
            int maxValueWithoutThisItem = getCachedValue(itemIdx-1,bagIdx,values);
            // 计算【当前背包size下，如果当前物品可取时，背包可存放的最大价值】
            // 计算方法为：如果当前物品可以被当前背包size容纳
            //      那么尝试优先存放该物品，并从之前的不包含当前物品的结果中
            //          寻找【可以填满剩余空间的最大价值】，二者相加即为结果。
            int maxValueIncludeThisItem = itemSizes[itemIdx] <= thisBagSize ?
                    itemValues[itemIdx] + getCachedValue(itemIdx-1,thisBagSize-itemSizes[itemIdx]-1,values): maxValueWithoutThisItem;
            // 比较【当前背包size下，如果当前物品不可取时，背包可存放的最大价值】和【当前背包size下，如果当前物品可取时，背包可存放的最大价值】
            // 哪个大就选择哪个值作为当前阶段的解。
            values[itemIdx][bagIdx] = Math.max(maxValueWithoutThisItem,maxValueIncludeThisItem);
        }
    }
    return values[itemsNum-1][bagSize-1];
}
private int getCachedValue(int i,int j,int[][] values){
    if (i < 0 || j < 0){
        return 0;
    }

    return values[i][j];
}

2.2 最长公共子串

2.2.1 题目

【描述】：给出两个字符串，找到最长公共子串，并返回其长度。

子串的字符应该连续的出现在原字符串中，这与子序列有所不同。

【样例 1】:

输入: “hish” and “fish”
输出: 3
解释: 最长公共子串是 “ish”

【样例 2】:

输入: “hish” and “vista”
输出: 2
解释: 最长公共子串是 ‘is’

2.2.2 题解

将两个单词的字母分列为横纵轴，如下图所示。

因为公共子串有顺序和连续的要求（如is和si就不是一个公共子串，ios和is不是一个共同子串，只有is和is才是。），所以在矩阵当中，两个相邻的对角线的单元格都为1的时候，才是公共子串出现的时候。

那我们把两个相邻的成对角线的单元格都赋值1可以吗？不行，还记得我们动态规划状态的定义吗？状态是过去阶段的总结！

所以，我们应该用右下角的单元格来存储目前已出现的这个公共子串的长度，而不是单纯的赋值1。

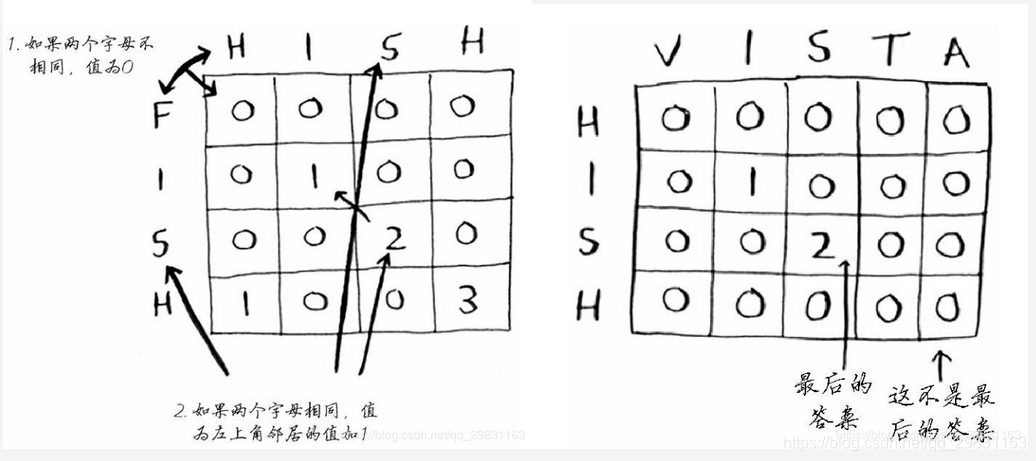
对于前面的背包问题，最终答案总是在最后的单元格中。但对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中。

2.2.3 代码

/** 最长公共子串
 * @param Str1: Str1 string
 * @param str2: str2 string
 * @return: the length of the longest common substring
 */
public int longestCommonSubstring(String str1, String str2) {
    int result = 0;
    if (str1.isEmpty()|| str2.isEmpty()){
        return result;
    }
    // 创建一个数组，存放已计算过的结果，填表法。
    int[][] values = new int[str1.length()][str2.length()];
    for (int i = 0;i<str1.length();i++){
        for (int j = 0;j<str2.length();j++){
            // 状态转移方程为：当两个字母相等时，当前值取左上角的单元格的值+1
            if (str1.charAt(i) == str2.charAt(j)){
                values[i][j] = getCachedValue(i-1,j-1,values)+1;
            }
            result = Math.max(result,values[i][j]);
        }
    }
    return result;
}
private int getCachedValue(int i,int j,int[][] values){
    if (i < 0 || j < 0 || i >= values.length || j >=values[0].length){
        return 0;
    }
    return values[i][j];
}

2.3 最长公共子串

2.3.1 题目

【描述】：给出两个字符串，找到最长公共子序列(LCS)，返回LCS的长度。

最长公共子序列的定义：

最长公共子序列问题是在一组序列（通常2个）中找到最长公共子序列（注意：不同于子串，LCS不需要是连续的子串）。该问题是典型的计算机科学问题，是文件差异比较程序的基础，在生物信息学中也有所应用。

【样例 1】:

输入: “fosh” and “fort”
输出: 2
解释: 最长公共子序列是 “f”,”o”

【样例 2】:

输入: “fosh” and “fish”
输出: 3
解释: 最长公共子序列是 “f”,”s”,”h”

2.3.2 题解

将两个单词的字母分列为横纵轴，如下图所示。

因为公共子序列有顺序的要求，但是没有连续的要求（如is和si就不是一个公共子序列，但ios和is中的is是公共子序列），所以在矩阵当中，某个字母相等的单元格的左上部分存在另一个字母相等的单元格，才是公共子序列出现的时候。

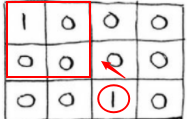
但因为公共子序列没有连续的要求，故而两个1，可能离得有点远，没法像最长公共子串那一题一样直接根据左上相邻单元格来判断，所以在该题状态转移方程中，我们要注意将1一直传递下去。

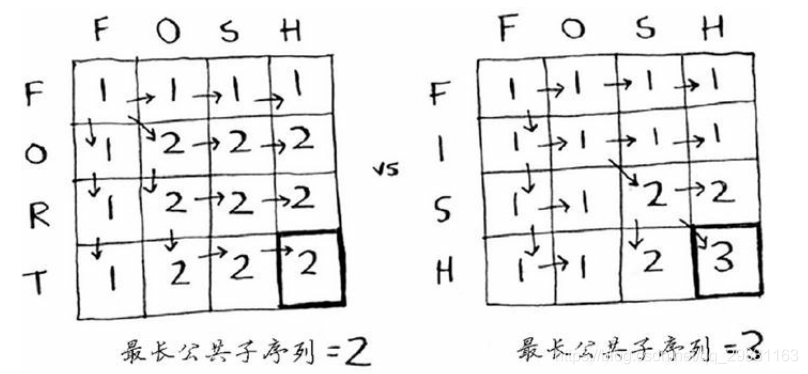
所以我们得到状态转移方程：

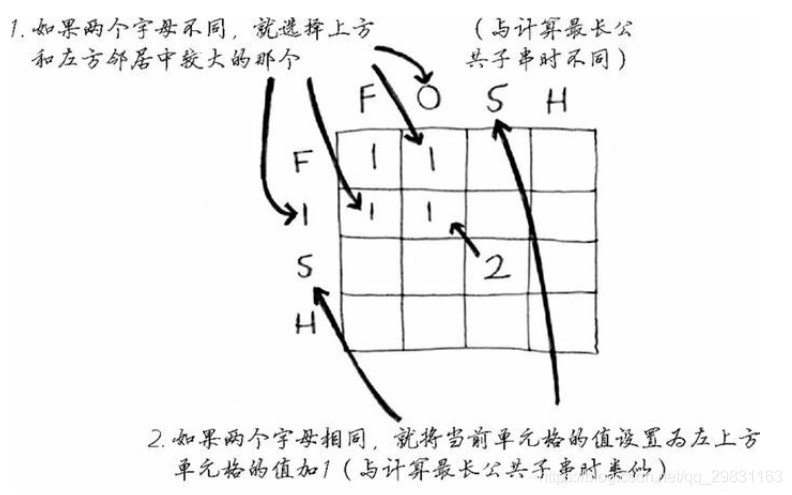
2.3.3 代码

/** 最长公共子序列
 * @param Str1: Str1 string
 * @param str2: Str1 string
 * @return: The length of longest common subsequence of Str1 and str2
 */
public int longestCommonSubsequence(String Str1, String str2) {
    int result = 0;
    if (Str1.isEmpty()|| str2.isEmpty()){
        return result;
    }
    // 创建一个数组，存放已计算过的结果，填表法。
    int[][] values = new int[Str1.length()][str2.length()];
    for (int i = 0;i<Str1.length();i++){
        for (int j = 0;j<str2.length();j++){
            // 状态转移方程为：
            // 1. 当两个字母相等时，当前值取左上角的单元格的值+1
            // 2. 当两个字母不等时，当前值取左方和上方两个单元格中最大的值
            if (Str1.charAt(i) == str2.charAt(j)){
                values[i][j] = getCachedValue(i-1,j-1,values)+1;
            }else {
                values[i][j] = Math.max(getCachedValue(i,j-1,values),getCachedValue(i-1,j,values));
            }
            result = Math.max(result,values[i][j]);
        }
    }
    return result;
}
private int getCachedValue(int i,int j,int[][] values){
    if (i < 0 || j < 0){
        return 0;
    }
    return values[i][j];
}