JAVA中浮点型数据的存储方式

前言

在JAVA中，我们知道int和float占用4个字节，double和long占用8个字节。

那为何int和long的取值范围分别是[-2^31,2^31]，float的取值范围却是[-3.40282346638528860e+38 , -1.40129846432481707e-45] ∪ [1.40129846432481707e-45 ~ 3.40282346638528860e+38]？（long和double同理）

或者我们看如下这道题：

public static void main(String[] args) {
	float f_v2 = 20.3f;
	float f_v3 = 20.5f;
	double d_v2 = 20.3d;
	double d_v3 = 20.5d;
	System.out.println(f_v2 == d_v2?"true":"false");
	System.out.println(f_v3 == d_v3?"true":"false");
}

答案是f_v2==d_v2为false，而f_v3==d_v3为true。

一切的原因，都要从java对于浮点型数据的存储说起。

我们开门见山，直接给出将十进制浮点数存储到内存空间中需要的步骤：

1. 将十进制浮点数转为二进制浮点数
2. 将二进制浮点数再转换成科学计数法
3. 优化空间，使用一些技巧，提升存储效率

1 将十进制浮点数转为二进制浮点数

计算机的存储是基于二进制的，要存储一个十进制浮点数，那么必然要先将这个其转为二进制。对于整数的十进制转二进制，我想我们大家都很熟悉，那么对于一个浮点数，十进制如何转为二进制呢？

浮点数可以分为三个部分：符号部分，整数部分，小数部分。

符号部分我们先不论，我们来看一个浮点数20.3:

整数部分：

整数部分是20，转二进制变成10100

小数部分：

小数部分是0.3，小数转为二进制，在java中有如下规则：

1. 将小数部分乘2,得到一个小数res。
2. 取res的整数部分为当前bit的值。
3. 再取res的小数部分接着乘2。
4. 重复上述过程，直至最后没有小数或者小数出现循环。

以0.3为例：

0.3 * 2 = 0.6 (取整数0)

0.6 * 2 = 1.2 (取整数1)

0.2 * 2 = 0.4 (取整数0)

0.4 * 2 = 0.8 (取整数0)

0.8 * 2 = 1.6 (取整数1)

0.6 * 2 = 1.2 (取整数1)

计算到这里，将再出现0.6，进入循环了，所以最终0.3的二进制结果是：0.3 = 0.01001 1001 1001...1001

所以20.3 = 10100.01001 1001 1001...1001

再以0.5为例：

0.5 * 2 = 1.0 (取整数1)

0 * 2 = 0 (取整数0)

计算到这里出现0了，计算结束。所以，转换后0.5 = 0.1

所以20.5 = 10100.1

2 将二进制浮点数转换成科学计数法

如果要把十进制浮点数，存储到内存空间中，也就是4或者8个字节中，那么还需要进一步将二进制的浮点数转换成科学计数法。

我们可以很容易得到以下等式

20.5(十进制) = 10100.1(二进制) = 1.01001E4(十进制科学计数) = 1.01001E100(二进制科学计数)

20.3(十进制) = 10100.01001 1001...1001(二进制) = 1.010011001...1001E4(十进制科学计数) = 1.010011001...1001E100(二进制科学计数)

这里E100指10的4次方，4也要二进制表示就是100；

用以科学计数法表示的1.01001 E 100举例，1.01001部分叫做尾数；E叫做基数，在科学计数法里E=10；100部分叫做指数；

那么我们要存储1.01001E100，要存哪些信息呢？

1. 尾数1.01001要存，如果遇到像0.3那样的无限循环的尾数，空间不够存储的部分直接舍弃就好，这也是为什么浮点数会有精度问题的原因。
2. 基数E不要存，因为E固定等于10。
3. 指数100要存。
4. 除此之外还有遗漏吗？当然，别忘了正负的符号，这也需要一个bit来存。

所以我们可以看到，float和double的存储结构是这样的：

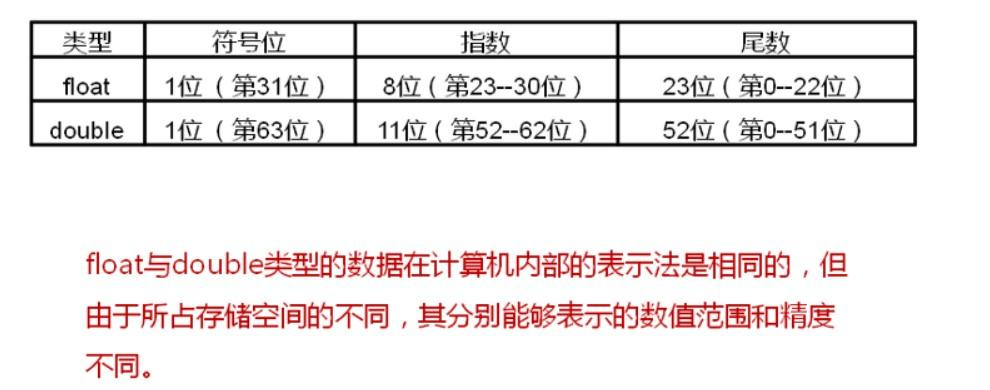
那么1.01001E100，我们是不是只要将符号位0、尾数位1.01001和指数位100分别存入对应空间就行了呢？当然这么存也是可以的，但为了节约空间，java设计了一些小技巧，使得空间的利用率更大。

3 优化空间

3.1 尾数的首位1舍弃

尾数1.01001要存，但不用全部都存，因为尾数第一位固定是1，我们没必要存，只要存.01001就行，这样就节省了一个bit。

3.2 指数位采用移位存储法

值得注意的是指数位的存储，float指数位有8bit，正常情况下，我们可以用常规的第一个bit表示符号，后面7个bit表示数值的存法，这样存储的指数值从-2^7到2^7。（double同理）

然而java中对指数位，采用的是移位存储法，即指数值的二进制，先加上127（float）或者1023（double），再存储。

如1.01001E100中指数是100，存入float中，那么要先加127：

  00000100
 +01111111
———————————
 +10000011

所以20.5存储在float中是这样的: 0 | 10000011 | 01001 00000 00000 00000 000

为什么不用传统的存储法，而要采用移位存储法呢？因为传统的存储法，0 000000和1 000000都表示十进制的0，只不过前者是+0，后者是-0；两个0含义相同，而float指数位只有8bit，最多只能表示256个数，现在两个等价的0占用了两种表示方法，那就有一种表示方法被浪费了。而使用移位存储法，则没有正负0的问题，不会造成浪费。

4 结语

最后回到我们在前言的题目：为什么2.3f==2.3d为false，而2.5f==2.5f为true。

我们可以知道：

• 2.5的存储是：
  • float：0 | 10000011 | 01001000....（补0直到23位）
  • double：0 | 1000 000 0011 | 01001....（补0直到52位）
• 2.3的存储是：
  • float：0 | 10000011 | 010011001...（循环直到23位）
  • double：0 | 1000 000 0011 | 010011001...（循环直到52位）

在先强转后比较的时候，比如float转成double，会将指数部分先-127，得到原始的指数二进制值，再将其+1023，得到double类型的指数值，位数不足的在高位补零。double转为float同理。所以强转和比较，指数部分是没有问题的。

重点就在于尾数部分，float转成double，会在尾数的后面补0，double转为float，则删掉后面多余的尾数位。

对于2.5来说，转换时增删的部分都是0，所以不影响比较的大小。

而对于2.3来说，增删的部分，删掉的是循环的1001，增的却是0，这就导致了2.3f和2.3d的尾数部分不相等。